Inorganic Crystal Structure Determination by X-ray Diffraction: From Foundational Principles to AI-Driven Advances

Abstract

This article provides a comprehensive overview of inorganic crystal structure determination using X-ray diffraction, tailored for researchers and drug development professionals. It explores the foundational principles of crystallography, details both traditional and cutting-edge methodologies like the AI-powered PXRDGen and XDXD models, and addresses key challenges such as peak overlap and light atom localization. The content also covers critical validation protocols to ensure structural accuracy and compares different analytical techniques. By synthesizing the latest advancements, this guide serves as a vital resource for accelerating materials discovery and innovation in biomedical research.

The Bedrock of Crystallography: Core Principles of Inorganic Structure Analysis

Bragg's Law and the Fundamentals of X-ray Diffraction

Core Principles and Theoretical Foundation

X-ray Diffraction (XRD) is a powerful non-destructive analytical technique that provides unparalleled insights into the atomic and molecular structure of crystalline materials [1]. The technique relies on the fundamental principle that when a monochromatic X-ray beam interacts with a crystalline material, it is diffracted by the periodic lattice of atoms in specific, predictable directions [2]. This phenomenon occurs because the wavelength of X-rays (approximately 0.1-10 nm) is comparable to the spacing between atoms in crystal structures, allowing them to interact constructively with the atomic planes [1].

Bragg's Law: The Cornerstone of XRD

The entire framework of XRD analysis is built upon Bragg's Law, formulated in 1913 by Sir William Henry Bragg and his son Sir William Lawrence Bragg, who later received the Nobel Prize in Physics in 1915 for this foundational work [2]. Bragg's Law mathematically describes the condition under which constructive interference of X-rays occurs when they interact with parallel crystal planes [1] [3].

The law is expressed by the equation: nλ = 2d sinθ [1]

Where:

• n = order of diffraction (an integer: 1, 2, 3...)
• λ = wavelength of the incident X-ray beam (typically 1.5418 Ã… for copper Kα radiation)
• d = interplanar spacing (the perpendicular distance between parallel crystal planes)
• θ = Bragg angle (the angle between the incident X-ray beam and the crystal plane)

This relationship establishes that diffraction occurs only when the path difference between X-rays scattered from parallel crystal planes equals an integer multiple of the X-ray wavelength [1]. Each set of planes, characterized by their Miller indices (hkl), will produce a diffraction peak at a specific angle 2θ where this condition is satisfied [1].

XRD Instrumentation and Experimental Methodology

The X-Ray Diffractometer

A modern X-ray diffractometer consists of several essential components that work in coordination to measure diffraction patterns [1] [2]:

• X-ray Source: Generates monochromatic X-rays through electron bombardment of a metal target, most commonly copper (Cu Kα, λ = 1.5418 Ã…) or molybdenum (Mo Kα, λ = 0.71 Ã…) [1].
• Incident Beam Optics: Conditions the X-ray beam using Soller slits for controlling beam divergence, monochromators for wavelength selection, and focusing mirrors for beam concentration [1].
• Sample Stage: Holds the specimen and allows precise positioning and rotation during measurement, providing accurate angular positioning potentially with environmental controls [1].
• Detector System: Records the diffracted radiation using position-sensitive detectors (PSDs) or area detectors that simultaneously collect data over a range of angles [1] [4].
• Goniometer: A precision mechanical system controlling angular relationships between X-ray source, sample, and detector with angular accuracy better than 0.001° [1].

The instrument operates by directing X-rays at the sample while rotating both sample and detector according to θ-2θ geometry, ensuring the detector captures diffracted beams at the correct angle for constructive interference [1].

Experimental Workflow for XRD Analysis

The following diagram illustrates the standard workflow for XRD analysis from sample preparation to data interpretation:

XRD Experimental Workflow

Sample Preparation Protocol

For powder XRD analysis, the sample must be finely ground to a homogeneous powder (typically <10 μm particle size) to ensure a random orientation of crystallites [1]. The powder is then mounted on a glass slide or in a capillary, with care taken to create a flat, uniform surface to minimize preferred orientation effects that can alter relative peak intensities [1].

Data Collection Parameters

Standard data collection parameters for routine phase analysis include [4]:

• Angular Range: 5-80° 2θ for most applications
• Step Size: 0.01-0.02° 2θ
• Counting Time: 0.5-2 seconds per step
• X-ray Source: Cu Kα radiation at 40 kV and 40 mA

For specialized applications like retained austenite quantification or residual stress measurement, specific standardized protocols must be followed according to international standards such as ASTM E915 and EN UNI 15305 [2].

Research Reagent Solutions and Essential Materials

Table 1: Essential Research Reagents and Materials for XRD Analysis

Item	Function	Specifications
X-ray Tubes	Generate monochromatic X-rays	Copper (Cu Kα, λ=1.5418 Å) for most applications; Molybdenum for heavy elements [1]
Sample Holders	Mount powdered specimens	Glass slides for flat plate; Capillaries for random orientation [1]
Certified Reference Materials	Instrument calibration and quantification	NIST standards for peak position and intensity calibration [2]
Single Crystal Substrates	Mount single crystal samples	Micromount loops and capillaries [1]
Incident Beam Optics	Condition X-ray beam	Soller slits, monochromators, focusing mirrors [1]

XRD Data Interpretation and Analysis

Understanding XRD Patterns

An XRD pattern displays diffraction intensity versus diffraction angle (2θ), where each peak corresponds to a specific set of parallel crystal planes characterized by Miller indices (hkl) [1]. The diffraction pattern serves as a unique fingerprint for each crystalline phase, enabling identification and quantitative analysis [1].

The key characteristics of XRD patterns provide comprehensive structural information [1]:

• Peak Position: Determined by the angular position that directly relates to d-spacing through Bragg's law; used to determine lattice parameters and identify phases.
• Peak Intensity: The height or integrated area indicates the atomic arrangement within the crystal structure and relative abundance of different phases.
• Peak Width: Reveals crystal quality, including crystallite size and microstrain effects; narrow peaks indicate large, well-formed crystals.
• Peak Shape: Provides insights into crystal defects, stacking faults, and other structural imperfections.

Phase Identification and Quantitative Analysis

Phase identification is performed by comparing the measured diffraction pattern with reference patterns in international databases such as the Powder Diffraction File (PDF-2) or the Crystallography Open Database (COD) [2]. Modern analysis software automates this comparison process for rapid and precise phase identification [2].

For quantitative phase analysis, several methodologies are employed:

• Reference Intensity Ratio (RIR) Method: Uses known intensity ratios between phases for quantification.
• Rietveld Refinement: A full-pattern fitting method that provides the most accurate quantitative results by refining structural parameters against the entire diffraction pattern [4].

Table 2: Key Applications of Bragg's Law in XRD Analysis

Application	Methodology	Information Obtained
Phase Identification	Matching d-spacings and intensities to reference patterns	Crystalline phases present in the sample [3]
Lattice Parameter Determination	Precise measurement of peak positions	Unit cell dimensions and crystal system [1]
Crystallite Size Analysis	Analysis of peak broadening using Scherrer equation	Average crystallite size and size distribution [2]
Residual Stress Measurement	Tracking d-spacing changes under stress	Strain and residual stress in materials [1]
Thin Film Characterization	Grazing Incidence XRD (GIXRD)	Crystal orientation, internal stress, and coating quality [2]

Advanced Applications in Inorganic Crystal Structure Determination

Residual Stress and Strain Analysis

Residual stress analysis is essential to ensure the reliability of mechanical components, steel structures, and materials subjected to welding, heat treatment, or plastic deformation [2]. XRD enables non-destructive measurement of these stresses by comparing lattice spacing variations with those of a stress-free reference [2]. This application is particularly valuable in metallurgy and materials engineering for assessing component lifetime and performance.

The relationship between strain and diffraction peak shift is derived from Bragg's law:

ε = (d - d₀)/d₀ = -cotθ × (θ - θ₀)

Where ε is the strain, d is the strained lattice spacing, d₀ is the unstrained lattice spacing, θ is the diffraction angle for the strained material, and θ₀ is the diffraction angle for the unstrained reference material.

Retained Austenite Analysis in Steels

Retained austenite is a metastable phase that can persist in steels after heat or mechanical treatment, significantly affecting properties such as hardness, fatigue strength, and dimensional stability [2]. XRD is the reference technique for quantifying retained austenite, distinguishing martensitic, ferritic, and austenitic phases with high precision [2]. This application is critical in steel production and heat treatment validation.

Thin Film and Coating Characterization

Using techniques like Grazing Incidence XRD (GIXRD), it is possible to characterize coatings and thin films with nanometric precision [2]. The analysis reveals information on crystal orientation, internal stress, and coating quality, which is essential for advanced materials development in electronics and functional coatings [2].

The following diagram illustrates the logical relationships in XRD structural determination and its connection to material properties:

XRD Structural Determination Logic

In-situ and Operando XRD Studies

Modern XRD instrumentation enables in-situ and operando studies of materials under non-ambient conditions, including high and low temperatures, controlled atmospheres, and under applied stress [4]. These advanced applications allow researchers to monitor phase transitions and structural changes in real-time, providing crucial insights into material behavior under realistic operating conditions.

Emerging Trends and Future Perspectives

XRD technology is undergoing rapid evolution, driven by the demand for compact, automated, and intelligent instruments [2]. According to market analysis, the global XRD market is expected to exceed $1 billion by 2033, driven by miniaturization, automation, and AI-powered software solutions [2].

Key innovations shaping the future of XRD include:

• Artificial Intelligence and Machine Learning: AI approaches are achieving over 90% accuracy in determining crystal phases and space groups from XRD data, eliminating the need for manual tuning [3]. Machine learning algorithms are also being applied to predict crystal size and microstrain from XRD data using Gaussian peak shape analysis [3].

• Advanced Detector Technology: Two-dimensional detectors enable quick collection of low-noise data, facilitating in-situ analysis of structural variations including phase transitions [3].

• Laboratory-based 3D Micro-beam XRD: Recent research introduces the Lab-3DμXRD method, enabling three-dimensional, non-destructive material characterization directly in laboratory environments [2].

• Integrated Workflows: The combination of robotics and AI-driven workflows are shaping the next generation of diffractometry—faster, smarter, and more accessible than ever before [2].

These technological advances continue to expand the applications of Bragg's Law and XRD analysis across scientific disciplines, from fundamental materials research to industrial quality control and pharmaceutical development. As instrumentation becomes more sophisticated and accessible, XRD remains an indispensable tool for inorganic crystal structure determination in research and industrial applications alike.

Understanding Unit Cells, Lattice Parameters, and Space Groups

The determination of inorganic crystal structures via X-ray diffraction research relies upon three foundational pillars: the unit cell, lattice parameters, and space groups. These concepts form the essential language through which the long-range periodic order of crystalline materials is described and quantified. The unit cell represents the simplest repeating volume that fully captures the crystal's symmetry and, when translated in three dimensions, generates the entire crystal lattice [5]. This fundamental building block is defined by its lattice parameters—the three edge lengths (a, b, c) and three interaxial angles (α, β, γ) that collectively specify its size and shape [6]. The specific values and relationships between these parameters determine the crystal system to which a material belongs, of which there are seven fundamental types [6].

The third critical component, space groups, provides a complete description of the crystal's internal symmetry by combining the translational symmetry of the Bravais lattice with the point group symmetry of atomic arrangements, along with possible screw axes and glide planes [7]. There exist exactly 230 three-dimensional space groups in classical crystallography, each defined by a specific set of symmetry operations [7]. The Hermann-Maguin notation system uses four symbols to uniquely specify each space group, beginning with a letter (P, I, R, F, A, B, or C) representing the Bravais lattice type, followed by symbols denoting the point group symmetries [7]. For inorganic crystal structure determination, precise understanding of the interrelationship between these three concepts is paramount, as the space group directly dictates the unique crystallographic positions within the unit cell and the resulting X-ray diffraction pattern [7].

Quantitative Framework of Crystal Systems

The classification of crystals into seven systems is governed by the specific relationships between their lattice parameters and angles, which directly correspond to increasing levels of symmetry. This systematic categorization enables researchers to quickly narrow down possible structures when analyzing X-ray diffraction data. The following table summarizes the defining characteristics of each crystal system:

Table 1: The Seven Crystal Systems and Their Defining Lattice Parameter Relationships

Crystal System	Lattice Parameter Relationships	Angle Relationships	Examples
Triclinic	a ≠ b ≠ c	α ≠ β ≠ γ ≠ 90°	K₂S₂O₈
Monoclinic	a ≠ b ≠ c	α = γ = 90° ≠ β	β-Sulfur, Selenium
Orthorhombic	a ≠ b ≠ c	α = β = γ = 90°	α-Sulfur, Iodine
Tetragonal	a = b ≠ c	α = β = γ = 90°	White Tin, Zircon
Trigonal	a = b = c	α = β = γ ≠ 90°	Calcite, Cinnabar
Hexagonal	a = b ≠ c	α = β = 90°, γ = 120°	Graphite, Zinc
Cubic	a = b = c	α = β = γ = 90°	Diamond, NaCl, Cu

For commonly encountered crystal structures, specific shorthand designations are often used. For instance, face-centered cubic (fcc) crystals like copper and aluminium belong to space group F M 3 M, while body-centered cubic (bcc) materials like iron and tungsten fall under space group I M 3 M [8] [7]. The hexagonal close-packed (hcp) structure, observed in magnesium and zinc, corresponds to space group P 6₃/M M C [7]. These conventions streamline communication among crystallographers and materials scientists.

Experimental Protocols for Crystal Structure Determination

Protein Crystallization and Sample Preparation

The process of determining biological macromolecule structures begins with protein crystallization, widely considered the rate-limiting step in most protein crystallographic work [6]. A reliable source of pure, homogeneous, and soluble protein is prerequisite, with typical protein concentrations ranging from 5 to 20 mg/mL. The crystallization process employs vapor diffusion methods (sitting drop or hanging drop) where 1-2 μL of protein solution is mixed with an equal volume of precipitant solution and equilibrated against a reservoir containing 500-1000 μL of precipitant solution [6]. Commercial sparse matrix screens systematically vary key parameters including precipitant type and concentration (e.g., polyethylene glycol, ammonium sulfate), buffer identity and pH, temperature, and additives. Successful crystallization typically yields crystals with minimum dimensions of 0.1 mm to provide sufficient crystal lattice volume for X-ray exposure [6]. Before data collection, crystals must be verified to contain the target macromolecule rather than precipitant salts through techniques such as polyacrylamide gel electrophoresis or test X-ray diffraction exposure.

X-Ray Diffraction Data Collection

Once suitable crystals are obtained and mounted on a goniometer head, X-ray diffraction data collection proceeds with the following protocol. The X-ray source can be either a laboratory-scale generator (producing characteristic copper Kα radiation at λ = 1.5418 Å) or a synchrotron beamline providing tunable, intense X-ray beams [6]. The crystal-to-detector distance is calibrated to capture diffraction spots up to the desired resolution, typically 1.5-3.0 Å for initial characterization, with higher resolution required for atomic-level detail (carbon-carbon bonds are approximately 1.5 Å) [6]. Modern data collection employs charge-coupled device (CCD) detectors or hybrid pixel array detectors that offer rapid readout times (seconds) and high sensitivity, a significant advancement over traditional X-ray film which required exposure times of 30-40 minutes at synchrotrons and many hours with laboratory sources [6]. For complete data sets, crystals are rotated through a specified angular range (as little as 35° for high-symmetry cubic crystals up to 180° for lower-symmetry monoclinic crystals) while collecting multiple diffraction images [6]. Cryogenic protection (100 K nitrogen stream) is standard practice to mitigate radiation damage during data collection.

Data Processing and Structure Solution

Following data collection, the resulting diffraction images are processed through a standard workflow to determine the crystal structure. The protocol begins with data integration using software packages like XDS or HKL-2000 to convert spot positions and intensities into a list of structure factor amplitudes (Fₒ) with associated uncertainties (σ(Fₒ)) [5] [6]. Subsequent scaling and merging of symmetry-equivalent reflections yields a unique set of structure factors. Initial analysis of the diffraction pattern reveals the unit cell dimensions and space group symmetry based on systematic absences [6]. The central challenge, known as the phase problem, arises because experimental measurements capture only the amplitude of diffracted waves while losing their phase information [5] [9]. Traditional approaches to solving the phase problem include:

• Molecular Replacement: Utilizes a known homologous structure as a search model [9]
• Direct Methods: Applies probabilistic relationships between structure factor amplitudes to derive initial phase estimates, effective primarily at high resolutions (<1.2 Ã…) [9]
• Anomalous Dispersion: Exploits wavelength-specific scattering from heavy atoms

Once initial phases are obtained, electron density maps are calculated and iteratively improved through alternating cycles of model building and refinement until the atomic model optimally fits both the experimental data and expected geometric constraints [5] [6].

Figure 1: Protein Crystallography Workflow

Advanced Computational Methods in Structure Determination

Deep Learning Approaches for Low-Resolution Data

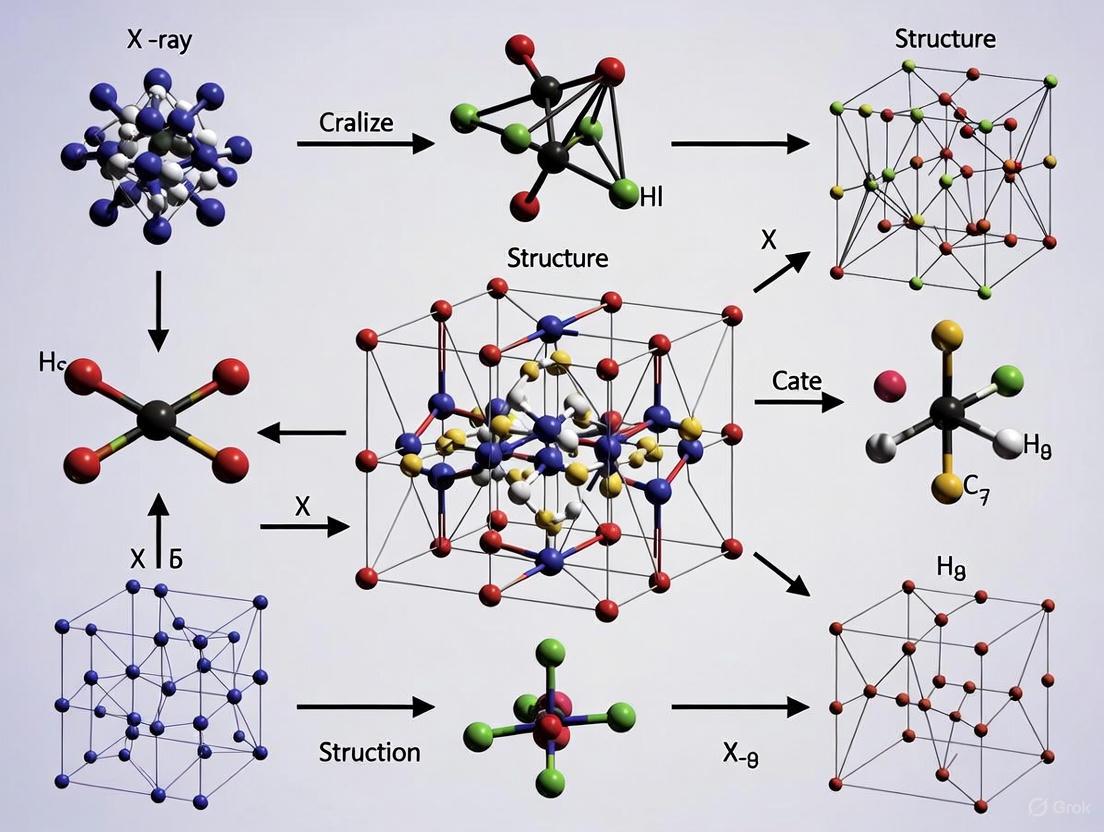
Recent advances in artificial intelligence have produced transformative computational methods for crystal structure determination, particularly when dealing with challenging low-resolution X-ray diffraction data. The XDXD framework represents a breakthrough as the first end-to-end deep learning model that predicts complete atomic structures directly from single-crystal X-ray diffraction data limited to 2.0 Ã… resolution [9]. This system employs a diffusion-based generative model conditioned on experimental diffraction patterns to produce chemically plausible crystal structures, bypassing the traditional need for manual electron density map interpretation [9]. When evaluated on 24,000 experimental structures from the Crystallography Open Database, XDXD achieved a 70.4% match rate with a root-mean-square error below 0.05, demonstrating remarkable accuracy even for systems containing 160-200 non-hydrogen atoms [9].

For powder X-ray diffraction data, where peak overlap presents significant analytical challenges, the PXRDGen system combines contrastive learning with generative models to achieve unprecedented accuracy [10]. This architecture integrates a pre-trained XRD encoder, a crystal structure generation module based on diffusion or flow models, and automated Rietveld refinement [10]. On the MP-20 dataset of inorganic materials, PXRDGen reached record match rates of 82% with a single sample and 96% with 20 samples, with root-mean-square errors approaching the precision limits of traditional Rietveld refinement [10]. These AI-driven methods effectively address longstanding challenges in crystallography, including localization of light atoms and differentiation of neighboring elements in the periodic table.

Database-Free Structure Creation Methods

For cases where database search fails to identify matching structures, the Evolv&Morph approach provides an innovative solution by combining evolutionary algorithms with crystal morphing to directly create structures reproducing target XRD patterns [11]. This method operates without prior knowledge from crystal structure databases, instead generating enormous numbers of candidate structures and selecting those maximizing the cosine similarity between their simulated XRD patterns and the target pattern [11]. The process applies Bayesian optimization to guide the morphing between structures, progressively improving the similarity score. For sixteen different crystal structure systems—twelve with simulated XRD patterns and four with experimental powder patterns—Evolv&Morph successfully created structures with cosine similarities of 99% for simulated targets and >96% for experimental patterns [11]. This demonstrates particular value for characterizing novel materials where database matches are unavailable.

Figure 2: AI-Driven Structure Determination

Essential Research Reagents and Materials

Successful crystal structure determination requires carefully selected reagents and materials throughout the experimental workflow. The following table details key components of the crystallographer's toolkit:

Table 2: Essential Research Reagents and Materials for Crystallography

Category	Specific Examples	Function & Purpose
Precipitants	Polyethylene glycol (PEG), Ammonium sulfate, 2-Methyl-2,4-pentanediol (MPD)	Induce protein crystallization by excluding water from solvation shell
Buffers	HEPES, Tris, Citrate, Phosphate buffers	Maintain specific pH environment optimal for crystal growth
Salts & Additives	Sodium chloride, Magnesium chloride, Lithium sulfate, Detergents	Modulate electrostatic interactions and improve crystal order
Cryoprotectants	Glycerol, Ethylene glycol, Sugars, Paratone-N oil	Prevent ice formation during cryocooling for data collection
Crystallization Plates	24-well sitting drop plates, 96-well sparse matrix screens	Enable high-throughput crystallization condition screening
Sample Mounting	Cryoloops, Micromounts, Capillary tubes	Secure crystals during X-ray exposure while minimizing background scattering
X-Ray Sources	Rotating anode generators, Synchrotron beamlines	Provide high-intensity X-ray illumination for diffraction experiments
Detectors	CCD detectors, Hybrid pixel array detectors	Record diffraction patterns with high sensitivity and dynamic range

The selection and optimization of these reagents profoundly impacts success rates in crystal structure determination projects. Commercial sparse matrix screens systematically combine these components to efficiently explore crystallization space, while specialized additives (e.g., divalent cations, heavy atoms) can be introduced to improve crystal quality or facilitate phasing [6].

The precise determination of inorganic crystal structures through X-ray diffraction research remains foundational to advances in materials science, pharmaceutical development, and molecular biology. The interrelationship between unit cells, lattice parameters, and space groups provides the theoretical framework for interpreting diffraction data and understanding atomic-scale organization in crystalline materials. While traditional crystallographic methods continue to yield vital structural insights, emerging computational approaches—particularly deep learning models and database-free structure creation—are dramatically accelerating and automating structure solution. These advanced protocols enable researchers to tackle increasingly challenging systems, from complex inorganic materials to biological macromolecules, pushing the boundaries of atomic-resolution structure determination. As these methodologies continue to evolve, they promise to unlock structural insights from previously intractable samples, further cementing X-ray crystallography's role as an indispensable tool for scientific discovery.

X-ray diffraction (XRD) stands as a cornerstone technique for determining the atomic-scale structure of crystalline materials, providing indispensable insights across scientific and industrial disciplines. Within inorganic chemistry and materials science, the choice between its two primary implementations—single-crystal X-ray diffraction (SCXRD) and powder X-ray diffraction (PXRD)—is critical and is dictated by sample properties and the specific structural information required. SCXRD provides the most definitive structural picture, enabling researchers to obtain unit cell parameters, space group, and full atomic coordinates from a single crystal [12]. In contrast, PXRD analyzes polycrystalline powders containing countless randomly oriented microcrystals, making it widely applicable but structurally less direct due to the loss of orientational information [1] [13]. This application note delineates the principles, capabilities, and protocols for these techniques, contextualized within inorganic crystal structure determination, to guide researchers and development professionals in selecting and implementing the appropriate methodology.

Comparative Technique Analysis

The following table summarizes the core characteristics and capabilities of SCXRD and PXRD, highlighting their respective advantages and limitations.

Table 1: Core Characteristics of Single-Crystal and Powder X-Ray Diffraction

Feature	Single-Crystal XRD (SCXRD)	Powder XRD (PXRD)
Sample Requirement	A single, high-quality crystal of sufficient size (typically > 10-50 µm) [12]	Polycrystalline powder (microcrystals randomly oriented) [1]
Primary Output	Complete 3D atomic model (electron density map) [12]	1D diffraction pattern (Intensity vs. 2θ) [1]
Structural Information	Full atomic coordinates, bond lengths/angles, thermal parameters, absolute configuration, disorder modeling [12] [14]	Phase identification, lattice parameters, crystallite size, strain, quantitative phase analysis [1]
Key Advantage	"Gold standard" for unambiguous, comprehensive structure determination [12]	High applicability; no need for single crystal growth; rapid phase analysis [1] [10]
Primary Limitation	Difficulty of growing a suitable single crystal [12]	Overlap of diffraction peaks (reflections) causes information loss, complicating structure solution [13] [10]
Typical Speed for Structure Solution	Fast: under a day with modern equipment/software [12]	Traditionally slow and labor-intensive; accelerated by new AI methods (seconds to minutes) [10]
Handling of Polymorphs	Can unambiguously define polymorphs and hydrates/solvates by revealing packing motifs [12]	Can identify mixtures of polymorphs and detect trace levels of alternate forms via pattern comparison [12]

Experimental Protocols

Protocol for Single-Crystal X-Ray Diffraction Analysis

The following workflow outlines the definitive method for determining a complete inorganic crystal structure.

Procedure Steps:

• Crystal Selection & Mounting: Select a single, well-formed crystal of the target inorganic compound under a microscope. The crystal must be of sufficient size (typically > 10-50 µm) and quality. Mount the selected crystal on a thin capillary loop using a viscous oil or directly on a fixed mount, ensuring it is centered [12] [14].
• Data Collection: Place the mounted crystal on the goniometer of a modern single-crystal diffractometer. The instrument will automatically center the crystal. Collect a full set of diffraction images by rotating the crystal through various angles (ω, φ, χ) while exposed to a monochromatic X-ray beam (e.g., Mo Kα or Cu Kα). The exposure time and rotation width are optimized for data completeness and resolution [12] [14].
• Data Reduction: Software processes the collected diffraction images to identify Bragg reflections, index them, and determine the unit cell parameters and Bravais lattice. Integrated intensities and estimated uncertainties for each reflection are obtained, resulting in a file of structure factor amplitudes (|F|) [14].
• Structure Solution: Using the reduced data, the phase problem is solved to generate an initial electron density map. For inorganic structures with heavy atoms, Patterson methods (e.g., SHELXT) are often effective. For lighter atom structures, Direct Methods (e.g., in SHELXT or OLEX2) may be employed. This step yields approximate positions for most, if not all, non-hydrogen atoms [14].
• Structure Refinement: The initial atomic model is refined against all collected diffraction data using a least-squares algorithm (e.g., SHELXL or OLEX2 refinemenet suite). Atomic coordinates, displacement parameters (Uiso/Ueq), and site occupancy factors are adjusted iteratively to minimize the discrepancy factor (R1). Anisotropic displacement parameters are typically used for all non-hydrogen atoms. The final model includes crystallographic data tables and a validated CIF (Crystallographic Information File) [12] [14].
• Validation & Reporting: The final structure is validated using checkCIF/IVT to ensure geometric and thermodynamic reasonableness. The CIF is deposited in a database (e.g., Cambridge Structural Database, ICSD), and a formal report, including tables of atomic coordinates, bond lengths, angles, and structure visualizations, is generated [14].

Protocol for Powder X-Ray Diffraction Analysis

This protocol covers both routine phase analysis and the more complex process of ab initio structure determination, highlighting the role of modern AI methods.

Procedure Steps:

• Powder Preparation: Grind the bulk inorganic sample into a fine, homogeneous powder using an agate mortar and pestle to minimize crystallite size effects and ensure a random distribution of orientations. Pack the powder uniformly into a sample holder (e.g., a flat plate or capillary), taking care to minimize preferred orientation, which can distort relative peak intensities [1].
• Data Collection: Load the prepared sample into a powder diffractometer. The instrument scans the sample through a range of Bragg angles (2θ), typically from 5° to 80° or higher, using monochromatic Cu Kα radiation. Modern diffractometers use position-sensitive detectors to collect data rapidly [1].
• Path A: Phase Analysis
  • Pattern Processing: The raw data is processed by smoothing, subtracting the background, and identifying the position (2θ), intensity, and full width at half maximum (FWHM) of all diffraction peaks [1].
  • Pattern Matching: The processed pattern is compared against a database of known reference patterns, such as the Powder Diffraction File (PDF). A successful match confirms the identity of the crystalline phases present. Quantitative phase analysis can be performed using the Rietveld method if the crystal structures of all components are known [12] [1].
• Path B: Structure Solution
  • Indexing & Space Group Determination: The positions of the first 20-40 peaks are used by indexing software (e.g., TOPAS) to determine the unit cell parameters. Subsequent analysis of systematic absences in the pattern allows for the determination of the space group. Machine learning models can also predict space groups and cell parameters directly from the pattern [10] [15] [16].
  • Structure Solution: This is the most challenging step. Traditional methods involve global optimization algorithms (e.g., simulated annealing, genetic algorithms) to find atomic positions that best match the observed intensities. Recently, end-to-end deep learning models like PXRDGen and CrystalNet have demonstrated the ability to solve structures directly from the PXRD pattern and chemical formula in seconds, achieving high accuracy [13] [10].
  • Rietveld Refinement: The initial structural model is refined against the entire experimental powder pattern (not just extracted intensities). Structural parameters (atomic coordinates, occupancies), profile parameters, and microstructural parameters (crystallite size, strain) are adjusted to achieve the best possible fit between the calculated and observed patterns [10] [16].

The Scientist's Toolkit: Essential Research Reagents & Materials

Table 2: Key Reagents, Materials, and Software for XRD Analysis

Item	Function / Application
High-Quality Inorganic Samples	The target material for analysis. Purity is critical for successful structure determination.
Agate Mortar and Pestle	For grinding and homogenizing bulk samples into fine powders for PXRD.
Silicon/Silicon Powder Standard	Used for instrument alignment and calibration in both SCXRD and PXRD.
Loop & Viscous Oil (e.g., Paratone-N)	For mounting and cryo-cooling single crystals on the diffractometer.
Capillaries & Flat Sample Holders	For mounting powder samples in PXRD experiments.
Crystallography Software (e.g., SHELX, OLEX2)	Industry-standard suite for SCXRD structure solution and refinement [14].
Powder Analysis Software (e.g., TOPAS, HighScore)	Software for PXRD data processing, phase identification, and Rietveld refinement.
AI-Powered Structure Solution Tools (e.g., PXRDGen, CrystalNet)	Next-generation deep learning models for solving crystal structures directly from PXRD data [13] [10].
Reference Databases (e.g., PDF, ICSD, CSD)	Essential for phase identification in PXRD and for comparing solved structures.
Bace1-IN-9	Bace1-IN-9|BACE1 Inhibitor|Research Compound
Pitavastatin-d4 (sodium)	Pitavastatin-d4 (sodium), MF:C25H23FNNaO4, MW:447.5 g/mol

SCXRD and PXRD are complementary techniques that form the bedrock of inorganic crystal structure determination. SCXRD remains the unequivocal "gold standard" for obtaining a complete, high-resolution atomic model when a suitable crystal is available, providing definitive data for research publications and intellectual property claims [12]. PXRD, while historically limited in its ability to solve novel structures, is indispensable for phase identification, quantification, and materials characterization in the absence of single crystals. The advent of artificial intelligence is dramatically reshaping the PXRD landscape, with models like PXRDGen and CrystalNet demonstrating that atomic-level structure determination from powder data alone is not only feasible but can be highly accurate and rapid [13] [10]. This advancement promises to automate a traditionally labor-intensive process, making robust crystal structure determination more accessible and accelerating discovery in inorganic chemistry and drug development.

The Critical Role of Crystallography in Materials Science and Drug Development

X-ray crystallography is a foundational analytical technique for determining the three-dimensional arrangement of atoms within crystalline substances. By analyzing the diffraction patterns produced when X-rays interact with a crystal, researchers can elucidate atomic-scale structures that are critical for understanding material properties and biological function [17]. This capability makes crystallography indispensable across scientific disciplines, from inorganic chemistry to pharmaceutical development. The technique's power lies in its ability to provide precise atomic coordinates, bond lengths, and bond angles, enabling researchers to establish structure-property relationships that drive innovation in materials design and drug discovery [18] [5].

Within inorganic chemistry, X-ray crystallography has been fundamental in developing key structural concepts, revealing bonding geometries, and explaining the unusual electronic or elastic properties of materials [17] [5]. Similarly, in pharmaceutical research, crystallography provides the structural basis for understanding drug-receptor interactions and enables structure-based drug design [6]. This article details the experimental protocols and applications of X-ray crystallography within the context of inorganic crystal structure determination, providing researchers with practical methodologies for advancing their work in materials science and drug development.

Core Principles of X-Ray Crystallography

X-ray crystallography is based on the principle that the regularly spaced atoms in a crystal lattice act as a diffraction grating for incident X-rays, producing a regular pattern of scattered radiation [17]. When X-rays strike a crystal, atoms scatter the incident radiation, and the scattered waves interact with one another through constructive and destructive interference. Constructive interference occurs only when the conditions of Bragg's Law are satisfied: nλ = 2d sinθ, where λ is the wavelength of the incident X-ray beam, d is the distance between crystal planes, θ is the angle of incidence, and n is an integer representing the order of diffraction [17] [18].

The fundamental repeating unit in any crystal is the unit cell, defined by six parameters: three side lengths (a, b, c) and three angles between them (α, β, γ) [17]. These parameters determine the crystal system, of which there are seven possible geometric shapes: triclinic, monoclinic, orthorhombic, tetragonal, trigonal, hexagonal, and cubic [6]. The specific arrangement of atoms within the unit cell, combined with the crystal system, generates a unique diffraction pattern that serves as a fingerprint for the crystalline material [17].

Table 1: The Seven Crystal Systems and Their Defining Parameters

Crystal System	Defining Parameters	Bravais Lattices
Triclinic	a ≠ b ≠ c; α ≠ β ≠ γ ≠ 90°	Primitive
Monoclinic	a ≠ b ≠ c; α = γ = 90°, β ≠ 90°	Primitive, Base-centered
Orthorhombic	a ≠ b ≠ c; α = β = γ = 90°	Primitive, Base-centered, Body-centered, Face-centered
Tetragonal	a = b ≠ c; α = β = γ = 90°	Primitive, Body-centered
Trigonal	a = b = c; α = β = γ ≠ 90°	Primitive
Hexagonal	a = b ≠ c; α = β = 90°, γ = 120°	Primitive
Cubic	a = b = c; α = β = γ = 90°	Primitive, Body-centered, Face-centered

Experimental Protocols for Inorganic Crystal Structure Determination

Sample Preparation and Crystallization

The initial and often most critical step in X-ray crystallography is obtaining high-quality single crystals of sufficient size for analysis. For inorganic compounds, common crystallization techniques include:

• Slow Evaporation: A solution of the compound is allowed to evaporate slowly at constant temperature, gradually increasing saturation until crystals form [18].
• Slow Cooling: A saturated solution at elevated temperature is slowly cooled, reducing solubility and promoting crystal growth [18].
• Vapor Diffusion: A solvent system in which the compound is insoluble is allowed to diffuse slowly into a solution of the compound, gradually reducing solubility [6].
• Crystallization from Melt: For high-temperature materials, the pure compound is melted and then slowly cooled below its melting point to form crystals.

For diffraction analysis, crystals typically need to be a minimum of 0.1-0.3 mm in their longest dimension to provide sufficient crystal lattice volume for exposure to the X-ray beam [6]. Before data collection, crystal quality should be verified through microscopic examination to ensure uniformity and lack of defects.

Data Collection Methods

Once suitable crystals are obtained, they must be properly mounted and aligned for data collection:

• Crystal Mounting: Crystals can be mounted in a capillary tube at room temperature or cryo-cooled in a stream of liquid nitrogen at approximately 100 K [6]. Cryo-cooling reduces radiation damage during data collection, potentially allowing complete data sets to be collected from a single crystal.

• X-ray Sources: Data can be collected using laboratory X-ray generators (producing X-rays via electrons striking a copper anode) or synchrotron sources, which provide more intense beams with higher quality optics [6]. Synchrotrons offer advantages for challenging crystallographic problems due to their intense, tunable X-ray beams.

• Detection Systems: Modern crystallography primarily uses imaging plate detectors or charged-coupled device (CCD) detectors, which offer high sensitivity and rapid readout times compared to traditional X-ray film [6].

The following workflow diagram illustrates the complete structure determination process for inorganic compounds:

Diagram 1: Workflow for inorganic crystal structure determination.

Data Analysis and Structure Solution

Data processing involves converting raw diffraction images into a set of structure factors that can be used to determine the electron density within the crystal:

• Data Reduction: Correcting for instrumental effects, absorption, and other experimental artifacts [18].

• Unit Cell Determination: Calculating the dimensions of the repeating unit in the crystal from the spacing and symmetry of diffraction spots [6].

• Space Group Determination: Identifying the crystal's space group from the systematic absences in the diffraction pattern [6].

• Structure Solution: Using techniques such as direct methods, Patterson methods, or charge flipping to obtain an initial model of the atomic positions [18].

• Structure Refinement: Iteratively improving the model against the experimental data using least-squares refinement until the agreement between observed and calculated structure factors is optimized [18].

Table 2: Key Crystallographic Databases for Inorganic Compounds

Database Name	Content Focus	Number of Entries	Access
Inorganic Crystal Structure Database (ICSD)	Inorganic crystal structures including pure elements, minerals, metals, and intermetallic compounds	>130,000 entries	Subscription
Cambridge Structural Database (CSD)	Organic and metal-organic structures	>300,000 entries	Subscription
American Mineralogist Crystal Structure Database	Mineral structures published in major mineralogy journals	Comprehensive mineral coverage	Free
Reciprocal Net	Molecular structures stored by research crystallographers	Varies	Free (Purdue member)

Applications in Materials Science

X-ray crystallography plays a transformative role in materials science by enabling researchers to correlate atomic-scale structure with macroscopic material properties. Key applications include:

Structure-Property Relationships

By determining precise atomic arrangements, researchers can understand and predict material behavior. For example, crystallography has revealed how the arrangement of atoms in high-temperature superconductors influences their superconducting properties [18]. Similarly, studies of zeolites and other porous materials have shown how their complex frameworks of silicon and aluminum atoms determine their catalytic and molecular sieve properties [18].

Materials Engineering and Design

The ability to determine crystal structures enables the rational design of new materials with tailored properties. Materials engineers use crystallographic data to modify material performance by manipulating crystal structures through doping, defect engineering, or creating composite structures [17]. This approach has led to advances in battery materials, photovoltaic cells, and thermoelectric materials.

Nanomaterial Characterization

X-ray crystallography has been adapted to study nanostructured materials, providing information about nanoparticle size, shape, and composition [18]. While traditional single-crystal X-ray diffraction (SCXRD) requires larger crystals, complementary techniques like powder X-ray diffraction (PXRD) and electron crystallography (EC) can be applied to nanocrystalline materials that are too small for conventional SCXRD [19].

The relationship between crystallographic analysis and materials development is illustrated below:

Diagram 2: Crystallography applications in materials science.

Applications in Drug Development

In pharmaceutical research, X-ray crystallography provides critical structural information that drives drug discovery and development:

Structure-Based Drug Design

The determination of three-dimensional protein structures, particularly with bound substrates or inhibitors, enables rational drug design [6]. Researchers can identify active sites, understand molecular recognition, and design novel compounds with optimized binding characteristics. This approach has revolutionized modern drug discovery, reducing the time and cost of bringing new therapeutics to market.

Protein-Ligand Interactions

Crystallography allows precise mapping of intermolecular interactions between drug candidates and their biological targets [6]. By visualizing hydrogen bonds, hydrophobic interactions, and van der Waals contacts, researchers can explain structure-activity relationships and guide medicinal chemistry optimization.

Polymorph Screening

Pharmaceutical compounds can exist in multiple crystalline forms (polymorphs) with different physical properties that affect drug stability, bioavailability, and manufacturability. X-ray powder diffraction is routinely used to identify and characterize polymorphs during drug development to ensure consistent product quality [17].

Table 3: Key Crystallographic Databases for Biological Macromolecules

Database Name	Content Focus	Number of Entries	Access
Protein Data Bank (PDB)	3D structures of proteins, nucleic acids, and complex assemblies	>200,000 entries	Free
Biological Macromolecule Crystallization Database (BMCD)	Crystallization conditions for macromolecules	Comprehensive	Free
Nucleic Acid Database (NDB)	Structural information about nucleic acids	~5,000 structures	Free

Research Reagent Solutions

Successful crystallographic studies require specific materials and reagents throughout the experimental workflow:

Table 4: Essential Research Reagents and Materials for X-Ray Crystallography

Reagent/Material	Function/Application	Specifications
High-Purity Inorganic Compounds	Sample synthesis and crystallization	≥99.9% purity, stoichiometrically defined
Crystallization Reagents	Promoting crystal growth	Precipitants (PEGs, salts), buffers, additives
Cryoprotectants	Preventing ice formation during cryo-cooling	Glycerol, paraffin oil, various cryoprotective solutions
Mounting Tools	Crystal manipulation and mounting	MicroLoops, capillaries, magnetic caps
X-Ray Transparent Tapes	Securing samples during data collection	Low-absorption adhesives
Calibration Standards	Verifying instrument performance	Silicon powder, corundum standards

Advanced Techniques and Future Directions

The field of X-ray crystallography continues to evolve with technological advancements:

Complementary Methods for Complex Structures

For crystals that are too small for conventional SCXRD or too complex for PXRD, electron crystallography (EC) provides a valuable complementary approach [19]. Recent developments in three-dimensional electron diffraction techniques, such as automated electron diffraction tomography (ADT) and rotation electron diffraction (RED), have enabled structure determination from nanocrystals [19].

Time-Resolved Crystallography

Using advanced X-ray sources like X-ray free electron lasers (XFELs), researchers can now study short-lived intermediate states in chemical and biological processes, providing insights into reaction mechanisms [19].

Combined Approaches

Increasingly, complex structural problems require the integration of multiple techniques. Combining X-ray diffraction with electron microscopy, spectroscopy, and computational methods provides a more comprehensive understanding of material properties [19].

The following diagram illustrates how different techniques complement each other for solving complex structural problems:

Diagram 3: Complementary structure-solving techniques.

Modern Methodologies: From Traditional Refinement to AI-Powered Structure Solution

Rietveld Refinement for Powder Diffraction Data

Rietveld refinement is a powerful computational technique for characterizing crystalline materials from powder diffraction data. First described by Hugo Rietveld, this method represents a full pattern fitting approach where a theoretical line profile is iteratively adjusted until it closely matches the measured experimental profile. Unlike traditional methods that analyze individual peaks in isolation, Rietveld refinement simultaneously analyzes the entire diffraction pattern, enabling the extraction of detailed structural and microstructural information. This methodology has become indispensable across numerous scientific disciplines involving crystalline materials, including materials science, chemistry, geology, and pharmaceutical development [20].

The fundamental principle underlying Rietveld refinement is the calculation of a complete powder diffraction pattern based on a structural model, which includes crystallographic parameters, peak shape descriptions, and background characteristics. This calculated pattern is then compared to the observed experimental data, and the differences between them are minimized through a least-squares refinement process. The method's versatility allows researchers to determine not only phase composition but also detailed structural parameters, anisotropic characteristics, crystallite size, microstrain, and atomic displacement parameters [20]. For inorganic crystal structure determination, Rietveld refinement provides a comprehensive approach to solving complex structural problems that are common in materials research.

Theoretical Foundation

Fundamental Principles

The Rietveld method operates on the premise that every point, y{i}(obs), in the observed powder diffraction pattern can be expressed as a function of the Bragg angle, *θ*{i}, and represents a combination of contributions from Bragg reflections from all crystalline phases plus a background intensity. The calculated intensity, y_{i}(calc), at each point i is given by:

y{i}(calc) = *y*{i}(bkg) + S Σ K |F{K}|² *Φ* (2*θ*{i} - 2θ{K}) *P*{K} A

where y{i}(bkg) is the background intensity, *S* is the scale factor, *K* represents the Miller indices (*hkl*) for Bragg reflections, *F*{K} is the structure factor, Φ is the reflection profile function, P{K} is the preferred orientation function, and *A* is the absorption factor. The structure factor *F*{K} is fundamentally related to the atomic arrangement within the crystal structure and is calculated as:

F{K} = Σ *f*{j} exp[2πi(hx{j} + *ky*{j} + lz{j})] exp[-*B*{j}(sinθ/λ)²]

where f{j} is the atomic scattering factor, (*x*{j}, y{j}, *z*{j}) are the fractional coordinates of atom j in the unit cell, and B_{j} is its temperature factor [20].

The refinement process systematically varies parameters in the calculated pattern to minimize the difference between the observed and calculated profiles. This is achieved by minimizing the residual function:

R = Σ w{i} [*y*{i}(obs) - y_{i}(calc)]²

where w{i} is the statistical weight, typically taken as 1/*y*{i}(obs). The quality of the refinement is assessed using various agreement indices, including the profile R-factor (R{p}), weighted profile R-factor (*R*{wp}), expected R-factor (R_{exp}), and the goodness-of-fit (GOF) indicator [20].

Quantitative Phase Analysis

The Rietveld method has revolutionized quantitative phase analysis (QPA) of crystalline mixtures by providing a "standardless" approach that uses crystal structure descriptions of each component to calculate their respective diffraction patterns. The weight fraction (W_{k}) of phase k in a multiphase mixture is determined using the equation:

W{k} = (*s*{k}Z{k}*M*{k}V{k}) / Σ (*s*{i}Z{i}*M*{i}V_{i})

where s is the Rietveld scale factor, Z is the number of formula units per unit cell, M is the mass of the formula unit, and V is the unit-cell volume [20]. This approach has been successfully applied to various challenging systems, including inorganic crystalline phases, organic compounds, and mixtures containing amorphous content [21].

The accuracy of Rietveld quantitative phase analysis depends on several factors, including radiation choice, sample preparation, and data collection strategies. Comparative studies have demonstrated that high-energy Mo Kα1 radiation often yields slightly more accurate analyses than conventional Cu Kα1 radiation, despite the latter's approximately ten times higher diffraction intensity. This improved accuracy with Mo radiation is attributed to the larger irradiated volume (approximately 100 mm³ for Mo transmission geometry versus 2 mm³ for Cu reflection geometry) and reduced systematic errors associated with higher energy radiation [21].

Current Methodologies and Advances

Traditional Approaches and Considerations

Traditional Rietveld refinement requires careful attention to numerous experimental and computational factors to ensure accurate results. Sample preparation is particularly critical, as the reproducibility of peak intensity measurements is governed by particle statistics. This can be improved by using short-wavelength radiation, continuous sample spinning during data collection, and careful milling to reduce particle size without inducing amorphization or excessive peak broadening [21].

The choice of radiation source significantly impacts refinement quality. As highlighted in Table 1, different radiation types offer distinct advantages and limitations for specific applications. For inorganic materials with high absorption coefficients, Mo Kα1 radiation often provides superior results due to deeper penetration and reduced microabsorption effects, despite its lower diffraction power compared to Cu Kα1 radiation [21].

Table 1: Comparison of X-ray Radiation Sources for Rietveld Refinement

Radiation Type	Wavelength (Ã…)	Irradiated Volume	Relative Intensity	Best Applications
Cu Kα1	1.5406	~2 mm³ (reflection)	10.2× (reference)	General purpose, organic materials
Mo Kα1	0.7093	~100 mm³ (transmission)	1×	Inorganic materials, high absorption
Synchrotron	Variable (e.g., 0.4959-0.7744)	Variable	Extremely high	High-resolution, complex structures

The limits of detection and quantification represent important considerations in Rietveld QPA. For well-crystallized inorganic phases using laboratory powder diffraction, the limit of quantification (LoQ) is approximately 0.10 wt% in stable fits with good precision. However, at this concentration level, accuracy remains poor with relative errors approaching 100%. Only contents higher than 1.0 wt% typically yield analyses with relative errors below 20%. The limit of detection (LoD) is approximately 0.2 wt% for Cu radiation and 0.3 wt% for Mo radiation under similar recording conditions [21].

Artificial Intelligence and Machine Learning Advances

Recent advancements in artificial intelligence have revolutionized powder diffraction crystal structure determination, addressing longstanding challenges in the field. The PXRDGen neural network represents a breakthrough approach that integrates pretrained XRD encoders with generative models to determine crystal structures with atomic accuracy (Table 2) [10].

Table 2: Performance Comparison of AI-Based Structure Determination Methods

Method	One-Sample Match Rate	Twenty-Sample Match Rate	Key Features	Applications
PXRDGen (Transformer encoder)	82%	96%	Conditional structure generation, Rietveld refinement	Inorganic materials, MP-20 dataset
PXRDGen (CNN encoder)	Higher than Transformer	N/A	Flexible pretraining parameters	Broad crystalline materials
CrystalNet	Not specified	Not specified	Variational query-based network	Cubic and trigonal systems
XtalNet	Not specified	Not specified	Contrastive learning, diffusion models	Complex MOF materials

PXRDGen employs an end-to-end neural network architecture that learns joint structural distributions from experimentally stable crystals and their corresponding powder X-ray diffraction patterns. The system comprises three key modules: a pretrained XRD encoder that aligns PXRD patterns with crystal structures using contrastive learning, a crystal structure generation module that produces atomic coordinates conditioned on PXRD features and chemical formulas, and a Rietveld refinement module that ensures optimal alignment between predicted structures and experimental data [10].

This AI-driven approach effectively tackles key challenges in powder XRD analysis, including the resolution of overlapping peaks, localization of light atoms (such as hydrogen or lithium), and differentiation of neighboring elements. Evaluation on the MP-20 inorganic dataset (containing experimentally stable inorganic materials with 20 or fewer atoms per primitive cell) demonstrates that PXRDGen achieves root mean square errors generally less than 0.01, approaching the precision limits of traditional Rietveld refinement but with significantly reduced human intervention and processing time [10].

Experimental Protocols

Sample Preparation and Data Collection

Proper sample preparation is crucial for obtaining high-quality powder diffraction data suitable for Rietveld refinement. The following protocol outlines the essential steps:

• Sample Grinding and Homogenization: Gently grind the sample using an agate mortar and pestle for approximately 20 minutes to ensure homogeneity. Avoid excessive grinding that may induce amorphous phases or alter crystallite size distribution [21].

• Particle Size Control: Achieve optimal particle statistics by reducing particle size to the 1-10 micrometer range. Verify appropriate sizing through microscopic examination or by monitoring peak broadening in preliminary diffraction patterns.

• Sample Loading: For reflection geometry (typically used with Cu Kα radiation), pack the powdered sample into a flat holder to ensure a smooth surface and minimize preferred orientation. For transmission geometry (often used with Mo Kα radiation), load the sample into a thin-walled capillary [21].

• Data Collection Parameters:

  • Cu Kα Radiation: Set voltage to 40 kV, current to 40 mA, step size to 0.02° 2θ, and counting time to 2-10 seconds per step depending on sample characteristics.
  • Mo Kα Radiation: Use voltage of 50 kV, current of 40 mA, step size of 0.01° 2θ, and longer counting times (10-30 seconds per step) to compensate for lower diffraction intensity [21].

• Angular Range: Collect data across a sufficient angular range (e.g., 5-80° 2θ for Cu Kα, 2-50° 2θ for Mo Kα) to ensure adequate reflection coverage for reliable refinement.

• Standard Measurement: Include a measurement of a certified standard material (such as NIST SRM 674b or LaB₆) under identical conditions for subsequent instrumental broadening correction [20].

Rietveld Refinement Workflow

The following step-by-step protocol describes the Rietveld refinement process for inorganic crystal structure determination:

Figure 1: Rietveld Refinement Workflow for Inorganic Materials

• Data Preparation: Import the raw diffraction data into the refinement software. Perform background subtraction, typically using a Chebyshev polynomial function with 5-12 coefficients. Apply corrections for instrumental aberrations if necessary [20].

• Initial Model Establishment: Obtain crystal structure models for all identified phases in the sample from crystallographic databases such as the Inorganic Crystal Structure Database (ICSD) or Crystallography Open Database (COD). For complex systems, begin with a single dominant phase and progressively add minor phases [20].

• Preliminary Refinement: Initiate refinement with the following sequence of parameters:

  • Scale factors for each phase
  • Zero-point shift correction
  • Unit cell parameters for each phase
  • Sample displacement errors

  At this stage, hold profile parameters and structural parameters at their initial values [20].

• Profile Parameter Refinement: Introduce peak shape parameters into the refinement process:

  • Gaussian (U, V, W) and Lorentzian (X, Y) components of profile coefficients
  • Preferred orientation parameters using March-Dollase or spherical harmonic functions
  • Background polynomial coefficients
  • Specimen transparency and roughness parameters [20]

• Structural Parameter Refinement: Once the profile matches satisfactorily, begin refining structural parameters:

  • Atomic coordinates (starting with heaviest atoms)
  • Isotropic temperature factors
  • Site occupancy factors for mixed occupancy sites
  • Anisotropic displacement parameters for well-ordered structures [20]

• Microstructural Analysis: For materials with broadened diffraction peaks, refine crystallite size and microstrain parameters using appropriate models (e.g., Thompson-Cox-Hastings pseudo-Voigt function). Note that accurate microstructural analysis requires prior instrumental broadening correction using standard reference materials [20].

• Validation and Assessment: Critically evaluate the refinement quality through:

  • Visual inspection of the difference plot
  • Analysis of agreement indices (R-factors and GOF)
  • Verification of chemical plausibility (bond lengths, angles, thermal parameters)
  • Statistical analysis of parameter uncertainties [20]

• Export Results: Document the final refinement parameters, quantitative phase composition, structural data, and microstructural characteristics for reporting and further analysis.

Accuracy Assessment and Troubleshooting

Assessing the quality of Rietveld refinement requires careful analysis of multiple indicators. The key agreement indices include:

• Profile R-factor (R{p}) = Σ|*y*{i}(obs) - y{i}(calc)| / Σ|*y*{i}(obs)|
• Weighted profile R-factor (R{wp}) = [Σ*w*{i}(y{i}(obs) - *y*{i}(calc))² / Σw{i}(*y*{i}(obs))²]^{1/2}
• Expected R-factor (R{exp}) = [(*N* - *P*) / Σ*w*{i}(y_{i}(obs))²]^{1/2}
• Goodness-of-fit (GOF) = (R{wp} / *R*{exp})²

where N is the number of observations and P is the number of refined parameters. Ideally, GOF should approach 1.0, with values below 4.0 generally considered acceptable for phase analysis [20].

Common refinement issues and their solutions include:

• High Background: Increase polynomial background coefficients or implement more sophisticated background models.
• Systematic Peak Shift: Refine zero-point error and specimen displacement parameters.
• Peak Asymmetry: Implement appropriate asymmetry correction functions.
• Poor Fit at Low Angles: Check for beam spillover, sample transparency, or primary beam divergence effects.
• Unexplained Peaks: Consider the presence of unidentified minor phases or impurities.
• Unphysical Structural Parameters: Verify the initial structural model and constraint strategies.

The Scientist's Toolkit

Essential Software and Databases

Table 3: Essential Resources for Rietveld Refinement

Resource	Type	Key Function	Availability
TOPAS	Software	Whole pattern fitting, Rietveld refinement, microstructure analysis	Commercial
EXPO	Software	Structure solution and refinement from powder data	Free
GSAS-II	Software	Comprehensive Rietveld analysis package	Free
FullProf	Software	Pattern matching, structure refinement, magnetic structures	Free
ICDD PDF-5+	Database	Reference diffraction patterns for phase identification	Commercial
ICSD	Database	Inorganic crystal structure data	Commercial
COD	Database	Open-access crystal structure database	Free
JADE Pro	Software	XRD pattern processing, quantification, and interpretation	Commercial
AChE/BChE-IN-4	AChE/BChE-IN-4|Dual Cholinesterase Inhibitor for Research	AChE/BChE-IN-4 is a dual acetyl- and butyrylcholinesterase inhibitor for Alzheimer's disease research. For Research Use Only. Not for human or veterinary use.	Bench Chemicals
Cortisone-d2	Cortisone-d2, MF:C21H28O5, MW:362.5 g/mol	Chemical Reagent	Bench Chemicals

Research Reagent Solutions

Table 4: Essential Materials for Rietveld Refinement Experiments

Material/Standard	Function	Application Context
NIST SRM 674b (CeOâ‚‚)	Instrumental broadening calibration	Crystallite size and strain analysis
LaB₆ (NIST SRM 660c)	Peak position and shape calibration	Instrument alignment and resolution assessment
Silicon Powder	Zero-angle and unit cell standard	Accuracy verification of diffraction angles
α-Al₂O₃ (Corundum)	Quantitative analysis standard	Reference material for phase quantification
Agate Mortar and Pestle	Sample homogenization	Particle size reduction and mixing
Sample Holders (Flat plate)	Sample presentation for reflection geometry	Standard measurement configuration
Capillary Tubes	Sample containment for transmission geometry	Measurements with Mo Kα radiation
Microcrystalline Cellulose	Diluent for low-absorbing samples	Reduction of absorption effects in organic materials

Rietveld refinement has evolved from a specialized structural analysis technique to a comprehensive methodology for powder diffraction data analysis. The integration of artificial intelligence, as demonstrated by systems like PXRDGen, represents a paradigm shift in how researchers approach crystal structure determination from powder data. These AI-driven methods achieve remarkable accuracy with minimal human intervention, potentially reducing structure solution time from days to seconds while maintaining precision approaching traditional Rietveld refinement [10].

For inorganic crystal structure determination, the careful selection of experimental parameters—particularly radiation type—combined with rigorous sample preparation and systematic refinement strategies remains essential for obtaining accurate results. The continued development of computational approaches, combined with established experimental protocols, ensures that Rietveld refinement will maintain its critical role in advancing materials research across scientific disciplines. As the field progresses, the integration of multimodal data sources and increasingly sophisticated computational methods promises to further enhance the power and accessibility of this indispensable technique for characterizing crystalline materials.

Overcoming the Phase Problem in Low-Resolution Data

The determination of inorganic crystal structures via X-ray diffraction (XRD) is fundamental to advancements in materials science, chemistry, and drug development. The central challenge in this process is the phase problem: while diffraction experiments measure the amplitudes of structure factors, the phase information is lost during measurement [22]. This loss renders the direct calculation of electron density maps impossible. The problem is particularly acute for low-resolution data (typically worse than 1.5-2.0 Ã…), which is common for complex inorganic materials, nano-crystals, or systems that are difficult to crystallize perfectly.

Traditional methods for phase determination, such as direct methods, require high-resolution data (better than 1.2 Ã…) and are often inadequate for larger unit cells or complex symmetries [9]. Experimental phasing through isomorphous replacement or anomalous scattering requires additional experiments and often heavy-atom derivatives, which can be non-trivial to obtain [23]. This application note outlines modern computational and experimental strategies designed to overcome these limitations, enabling robust structure determination from low-resolution diffraction data.

AI-Driven End-to-End Structure Determination

Recent breakthroughs in deep learning are reshaping the approach to the phase problem by bypassing traditional phasing and model-building steps altogether. These methods learn to directly map diffraction data to atomic models.

The XDXD Framework

The XDXD (X-ray Diffusion for structure Determination) framework is the first end-to-end deep learning model that predicts a complete atomic crystal structure directly from a single-crystal XRD pattern and chemical composition [9].

• Architecture: The model employs a diffusion-based generative architecture. It consists of an XRD encoder (based on transformer layers) that processes the diffraction signal, and a Diffraction-Conditioned Structure Predictor (DCSP) that iteratively refines atomic coordinates from random noise, conditioned on the diffraction data embeddings [9].
• Handling Data Uncertainty: To simulate experimental noise, the model is trained with random signal dropout, where 0-10% of diffraction signals are randomly removed [9].
• Performance: Evaluated on a benchmark of 24,000 experimental structures from the Crystallography Open Database (COD) with data limited to 2.0 Ã… resolution, XDXD achieves a 70.4% match rate with a root-mean-square error (RMSE) below 0.05. Its performance scales with complexity, maintaining a ~40% match rate even for systems with 160-200 atoms per unit cell [9].

Table 1: Performance Metrics of the XDXD Model on Low-Resolution (2.0 Ã…) Data

Number of Non-Hydrogen Atoms (per unit cell)	Match Rate (%)	Typical RMSE
0 - 40	~90 (estimated)	Low (<0.05)
40 - 80	~80 (estimated)	Moderate
80 - 120	~65 (estimated)	Moderate
120 - 160	~50 (estimated)	Slightly Higher
160 - 200	~40	Slightly Higher

The PXRDGen Framework for Powder Data

For powder X-ray diffraction (PXRD) data, which suffers from peak overlap and reduced information content, the PXRDGen model provides a state-of-the-art solution [10].

• Architecture: PXRDGen integrates a pre-trained XRD encoder, a crystal structure generation module (using diffusion or flow-based models), and an integrated Rietveld refinement module. The XRD encoder uses contrastive learning to align the latent space of PXRD patterns with crystal structures [10].
• Performance: On the MP-20 dataset of inorganic materials, PXRDGen achieves record-breaking match rates of 82% (1-sample) and 96% (20-samples) for valid compounds. The RMSE for atomic coordinates is generally less than 0.01, approaching the precision limits of Rietveld refinement [10].

The workflow for these AI-based structure determination methods is summarized below.

Advanced Computational & Experimental Protocols

Ab Initio Phasing via Solvent Flatness Constraint

For high-solvent-content crystals (solvent fraction >70%), a powerful ab initio phasing protocol exists that treats phasing as a constraint satisfaction problem [24].

• Principle: The method relies on the solvent flatness constraint—the concept that the solvent region in a protein crystal is largely featureless. When the solvent volume fraction is sufficiently high, this constraint provides enough redundancy to uniquely determine the electron density using only the diffraction amplitudes [24].
• Algorithm: The Difference Map algorithm, an iterative projection algorithm (IPA), is used. It iterates between real space (applying constraints like solvent flatness and positivity) and Fourier space (enforcing agreement with measured amplitudes). This algorithm has superior global convergence properties compared to conventional iterative density modification [24].
• Workflow:
  • Low-Resolution Envelope Determination: The molecular envelope is first approximated using only the lowest-resolution data.
  • Full-Resolution Phase Determination: All available data are used for phase determination, with the molecular envelope continuously updated.
  • Clustering and Consensus: Multiple runs with random starting phases are performed. A clustering procedure identifies consistent results, which are averaged to produce a consensus solution [24].
• Application Scope: This method has been successfully demonstrated on 42 known structures with solvent fractions of 0.60–0.85. It works robustly at intermediate resolutions (1.9–3.5 Ã…) but is most reliable with solvent fractions greater than 0.70 [24].

Directed Soaking for Experimental Phasing

For systems where computational phasing is challenging, a robust experimental method called "directed soaking" can be employed to obtain high-quality experimental phases [23].

• Principle: This strategy rationally engineers a specific high-affinity binding site for a heavy-atom compound directly into the RNA helix. This replaces the traditional "soak and pray" method with a reliable and predictable derivatization technique [23].
• Key Reagent: The method utilizes the G·U wobble pair motif, which creates a pocket in the RNA major groove that selectively binds trivalent cations like cobalt(III) hexammine, iridium(III) hexammine, or osmium(III) hexammine [23].
• Protocol:
  • Design and Insertion: An optimal version of the G·U motif, identified through crystallographic analysis, is inserted into the RNA helix of interest.
  • Crystallization and Soaking: The RNA is crystallized, and the crystal is soaked in a solution containing the hexammine complex.
  • Data Collection and Phasing: The bound heavy atom provides a strong anomalous signal, enabling phasing via Single-wavelength Anomalous Diffraction (SAD) or Multi-wavelength Anomalous Dispersion (MAD), even with in-house copper Kα radiation [23].

Table 2: Research Reagent Solutions for Directed Soaking

Reagent / Solution	Function in Protocol
Cobalt(III) Hexammine	Trivalent cation; binds specifically to engineered G·U motif; provides strong anomalous scattering signal for SAD/MAD [23].
Engineered G·U Wobble Pair Motif	RNA structural element; creates a high-affinity, high-occupancy cation binding site for rational derivatization [23].
Crystallization Chassis	A stable, well-characterized RNA/protein complex used to systematically test and crystallize different motif variants [23].

The Scientist's Toolkit

Table 3: Essential Software and Computational Tools

Tool Name	Type	Primary Function in Low-Resolution Structure Determination
XDXD	End-to-End Deep Learning Model	Directly generates complete atomic models from single-crystal XRD data and composition [9].
PXRDGen	End-to-End Deep Learning Model	Solves and refines crystal structures directly from PXRD data, handling peak overlap and light atoms [10].
Difference Map Algorithm	Iterative Projection Algorithm	Enables ab initio phasing for high-solvent-content crystals using constraints like solvent flatness [24].
Convolutional Neural Networks (CNN)	Deep Learning Architecture	Identifies constituent phases in complex multiphase inorganic compounds from their powder XRD patterns [25].
Lapatinib impurity 18-d4	Lapatinib Impurity 18-d4|Stable Isotope|	Lapatinib Impurity 18-d4 is a deuterium-labeled internal standard for precise LC-MS quantification of Lapatinib. For Research Use Only. Not for human or veterinary use.
Lycbx	Lycbx, MF:C33H42K2N6O11S3, MW:873.1 g/mol	Chemical Reagent

The phase problem in low-resolution X-ray diffraction data, once a major bottleneck in inorganic crystal structure determination, is now being overcome by a new generation of sophisticated methods. AI-powered end-to-end frameworks like XDXD and PXRDGen demonstrate that direct inference of atomic models from diffraction patterns is not only feasible but highly accurate. For ab initio scenarios, advanced iterative algorithms leveraging physical constraints like solvent flatness provide robust solutions, while experimental techniques like directed soaking offer a reliable path to experimental phases. Collectively, these protocols are transforming structural research, paving the way for the determination of increasingly complex and previously intractable inorganic materials.

Determining the atomic-level structure of crystalline materials is fundamental to advancements in drug development, materials science, and energy storage. For decades, solving crystal structures from X-ray diffraction (XRD) data, particularly from powdered samples (PXRD) or low-resolution single crystals, has been a labor-intensive process requiring significant expert intervention. Artificial intelligence is now transforming this field by enabling end-to-end structure determination. Two pioneering models, PXRDGen for powder diffraction and XDXD for low-resolution single-crystal data, represent significant breakthroughs in automating and accelerating this critical scientific process. These deep learning frameworks directly address longstanding challenges in crystallography, including the phase problem, overlapping peak resolution in powders, and interpretation of ambiguous low-resolution electron density maps [10] [26] [9].

Key Architectural Features

PXRDGen employs an integrated three-module architecture: a pre-trained XRD encoder that uses contrastive learning to align PXRD patterns with crystal structures, a conditional crystal structure generator based on diffusion or flow models, and an integrated Rietveld refinement module. This combination allows it to solve structures in seconds by learning joint structural distributions from experimentally stable crystals and their corresponding PXRD patterns [10] [27].

XDXD utilizes a diffusion-based generative framework conditioned on chemical composition and single-crystal XRD data. Its core innovation is a Diffraction-Conditioned Structure Predictor (DCSP) module that iteratively refines atomic coordinates. The model employs cross-attention mechanisms analogous to inverse Fourier transforms in crystallography, effectively bypassing the need for manual interpretation of ambiguous low-resolution electron density maps [26] [9].

Quantitative Performance Metrics

Table 1: Performance Comparison of AI Structure Determination Models

Model	Data Type	Test Dataset	Match Rate (1-sample)	Match Rate (Multi-sample)	RMSE	Key Innovation
PXRDGen	PXRD	MP-20 (Inorganic)	82%	96% (20 samples)	<0.01	Integration of generative structure prediction with Rietveld refinement
XDXD	Single-crystal XRD (2.0 Ã…)	COD (24,000 structures)	70.4%	N/A	<0.05	Direct atomic model prediction from low-resolution data
AI-PhaSeed	Single-crystal XRD	COD (P2₁/c)	N/A	N/A	N/A	Combines neural network phasing with traditional phase seeding

Table 2: Scope and Limitations of AI Crystallography Models

Model	Structure Types	Maximum System Size	Key Challenges Addressed	Typical Solution Time
PXRDGen	Inorganic crystals	20 atoms per primitive cell	Overlapping peaks, light atom localization, neighboring element differentiation	Seconds
XDXD	Organic, inorganic, peptides	200 non-hydrogen atoms per unit cell	Low-resolution data interpretation, phase problem	Minutes (including candidate ranking)
CrystalNet	Cubic/trigonal crystals	Varies	Reconstruction from powder data with minimal composition information	N/A

Performance evaluation reveals that PXRDGen achieves remarkable accuracy on the MP-20 dataset of inorganic materials, with Root Mean Square Error (RMSE) approaching the precision limits of traditional Rietveld refinement [10]. The model effectively addresses key challenges in powder diffraction, including resolving overlapping peaks, localizing light atoms, and differentiating neighboring elements [10] [27].

XDXD demonstrates robust performance across a diverse benchmark of 24,000 experimental structures from the Crystallography Open Database (COD), maintaining approximately 40% match rates even for complex systems containing 160-200 atoms per unit cell [9]. This scalability to larger systems highlights its potential for determining structures of pharmaceutical interest and complex organic molecules.

Experimental Protocols and Workflows

PXRDGen Structure Determination Protocol

Sample Preparation and Data Collection

• Prepare powdered crystalline sample according to standard PXRD protocols
• Collect PXRD pattern using standard laboratory diffractometer (Cu Kα radiation typically used)
• Determine unit cell parameters using conventional indexing software or integrated CellNet module
• Input chemical composition and PXRD pattern into PXRDGen framework

Structure Generation and Validation

• PXE module processes PXRD pattern using CNN or Transformer-based encoder
• CSG module generates candidate structures conditioned on PXRD features and chemical formula
• Multiple candidates generated using diffusion/flow-based sampling (typically 20 samples for optimal results)
• Automated Rietveld refinement optimizes structural parameters against experimental data
• Validate final structure using standard crystallographic metrics (R-factors, bond length/angle analysis)

XDXD Structure Determination Protocol

Data Preparation

• Collect single-crystal X-ray diffraction data (resolution up to 2.0 Ã… acceptable)
• Preprocess reflection data, extract structure factor amplitudes
• Input chemical composition and prepared diffraction data

Structure Generation and Selection

• XRD Encoder processes diffraction signals using transformer architecture
• Molecular Graph embedding layer encodes chemical information
• DCSP module performs iterative coordinate refinement through diffusion process
• Generate multiple candidate structures (typically 16) from random noise initialization
• Rank candidates by cosine similarity between simulated and experimental patterns
• Select top-ranked structure as final prediction

The Scientist's Toolkit: Essential Research Reagents and Materials

Table 3: Key Research Reagents and Computational Tools for AI-Enhanced Crystallography

Item/Resource	Function/Purpose	Application Context
Powder X-ray Diffractometer	Data collection for polycrystalline samples	PXRDGen input data generation
Single-crystal X-ray Diffractometer	High-quality reflection data collection	XDXD input data generation
MP-20 Dataset	Benchmark inorganic crystal structures	Training and validation of PXRDGen
Crystallography Open Database (COD)	Diverse experimental structures	Training and validation of XDXD
Rietveld Refinement Software	Structural parameter optimization	Integrated within PXRDGen workflow
Diffusion Model Framework	Generative structure prediction	Core of both PXRDGen and XDXD
Transformer/CNN Architectures	Feature extraction from diffraction patterns	XRD encoding in both models
L-Alloisoleucine-d10	L-Alloisoleucine-d10, MF:C6H13NO2, MW:141.23 g/mol	Chemical Reagent
INSCoV-600K(1)	INSCoV-600K(1), MF:C23H22ClF2N5O2S, MW:506.0 g/mol	Chemical Reagent

The development of PXRDGen and XDXD represents a paradigm shift in crystallographic structure determination, moving from expert-driven iterative approaches to automated, end-to-end solutions. These models demonstrate that deep learning can effectively overcome longstanding challenges in the field, particularly for difficult cases involving powder data or limited resolution. As these architectures evolve, their integration with traditional crystallographic methods and expansion to more complex systems—including pharmaceuticals, proteins, and nanomaterials—will further transform structural science. The achievement of atomic-level accuracy in seconds to minutes, rather than days to weeks, promises to accelerate discovery across scientific disciplines reliant on structural insights [10] [26] [9].

Performance Comparison of Modern Structure Determination Techniques

The field of inorganic crystal structure determination has been revolutionized by the integration of high-throughput methodologies and artificial intelligence. The following table summarizes the performance metrics of several state-of-the-art techniques as reported in recent literature.

Table 1: Performance metrics of recent structure determination techniques

Technique/Model Name	Input Data Type	Reported Match Rate	Key Advantages	Tested Material Systems
PXRDGen [10]	Powder XRD	82% (1-sample); 96% (20-samples)	Resolves overlapping peaks, locates light atoms, differentiates neighboring elements	MP-20 dataset (inorganic materials)
XDXD [9]	Single-crystal XRD (low-resolution, ≤2.0 Å)	70.4% (for 2.0 Å data)	End-to-end model; works directly from low-resolution data; handles 0-200 non-H atoms	24,000 structures from COD
CrystalNet [13]	Powder XRD + Composition	93.4% Avg. Structural Similarity	Successful even with partially-known chemical composition	Cubic and Trigonal crystal systems

Detailed Experimental Protocols

Protocol: Single-Crystal X-ray Diffraction for a Novel Ternary Indide

The following protocol outlines the procedure for determining the crystal structure of a new intermetallic compound, as exemplified by the study on ErCo2In [28].

Table 2: Key reagents and materials for synthesis and characterization

Research Reagent/Material	Specification/Purity	Primary Function
Erbium (Er) ingots	99.9 wt%	Rare-earth metal precursor providing the 'RE' site in the RECo2In structure.
Cobalt (Co) foil	99.99 wt%	Transition metal precursor.
Indium (In) tear drops	99.99 wt%	p-block metal precursor.
Argon Atmosphere	500 mbar	Inert gas for preventing oxidation during arc-melting.
Bruker D8 Venture Diffractometer	Mo Kα radiation	Instrument for collecting single-crystal X-ray diffraction data.

Procedure:

• Synthesis via Arc-Melting:

  • Weigh high-purity metals (Er, Co, In) in the stoichiometric ratio corresponding to the nominal composition (e.g., Er25Co50In25 for a 1:2:1 phase) for a total mass of ~1.0 g [28].
  • Load the metals into an arc-melting furnace. Seal and purge the chamber with argon gas to an atmosphere of 500 mbar.
  • Melt the sample. To ensure homogeneity, re-melt the sample button three times [28].
  • Monitor weight loss after melting; it should typically be less than 0.8% by mass [28].

• Post-Synthesis Annealing:

  • Seal the arc-melted button in an evacuated fused silica tube [28].
  • Anneal the sample at 1070 K (797 °C) for 720 hours (30 days) to achieve long-range atomic order and reach thermodynamic equilibrium [28].
  • After annealing, quench the sample by submerging the silica tube in cold water [28].

• Sample Preparation and Preliminary Analysis:

  • Crush a portion of the annealed sample to isolate single crystals suitable for X-ray diffraction [28].
  • For phase analysis, embed a separate portion in a mounting alloy (e.g., Wood's metal) and polish sequentially with sandpaper and diamond paste (1–5 μm grit) to create a flat, representative surface for SEM/EDX inspection [28].

• Single-Crystal X-ray Diffraction Data Collection:

  • Select a small, irregularly shaped single crystal from the crushed sample and mount it on a diffractometer (e.g., Bruker D8 Venture with monochromated Mo Kα radiation) [28].
  • Collect a full set of diffraction frame data at room temperature.
  • Integrate the raw data and apply absorption corrections using standard software packages (e.g., APEX3 and SADABS) [28].

• Structure Solution and Refinement:

  • Determine the space group from the observed extinction rules in the diffraction data (e.g., Pmma for ErCo2In) [28].
  • Solve the initial structural model using intrinsic phasing methods (e.g., SHELXT) [28].
  • Refine the structure using full-matrix least-squares refinement on F² (e.g., with SHELXL). Use standardized atomic coordinates from a known isostructural compound (e.g., TbCo2In for ErCo2In) as a starting model for the final refinement [28].
  • Refine all atomic displacement parameters anisotropically [28].
  • Deposit the final Crystallographic Information File (CIF) with a structural database (e.g., Cambridge Crystallographic Data Centre, CCDC) [28].

Protocol: AI-Assisted Structure Determination from Powder XRD Data

This protocol describes the use of the PXRDGen deep learning model for determining crystal structures directly from powder diffraction patterns, representing a shift towards automated analysis [10].

Procedure:

• Data Preparation:

  • Input Required: The experimental PXRD pattern and the chemical formula of the material [10].
  • Pre-processing: The PXRD pattern is fed into a pre-trained XRD encoder. Contrastive learning is used during pre-training to align the latent space of PXRD patterns with their corresponding crystal structures, enabling the encoder to extract meaningful features from the diffraction data [10].

• Crystal Structure Generation:

  • The extracted PXRD features and the chemical formula are passed to a Crystal Structure Generation (CSG) module [10].
  • The CSG module, which can be based on a diffusion or flow-based generative framework, uses this information to generate multiple candidate crystal structures [10].
  • Unit cell parameters can be provided to the model from conventional indexing software or predicted by an integrated Conditional Cell Generation network (CellNet) [10].

• Structure Validation and Refinement:

  • The candidate structures generated by the CSG module are automatically fed into a Rietveld refinement module within the PXRDGen framework [10].
  • This module refines the structural parameters to achieve the best possible fit between the theoretical XRD pattern of the candidate structure and the experimental input data [10].
  • The final output is an atomically accurate crystal structure that has been validated against the experimental pattern [10].

Workflow Visualization

The following diagram illustrates the automated, end-to-end workflow of the PXRDGen model for determining crystal structures from powder diffraction data [10].

Case Study: Resolving the Coloring Problem in RECo2In Structures

A significant challenge in intermetallic crystallography is the "coloring problem," where different atomic species can occupy the same crystallographic sites, leading to ambiguous structural models. This is prominently featured in the RECo2In (Rare Earth - Cobalt - Indium) series [28].

• The Problem: The TbCo2In-type and PrCo2Ga-type structures share the same space group (Pmma) and Wyckoff sequence (f2ea), differing only in whether the transition metal (Co) or p-block element (In/Ga) occupies specific 2f and 2e sites. These models are often indistinguishable by standard powder XRD analysis alone [28].
• The Solution: For ErCo2In, this ambiguity was resolved by:
  • Using single-crystal XRD, which provides superior data quality.
  • Employing materials informatics tools like the Crystal Bond Analyzer (CBA) for high-throughput analysis of bonding interactions.
  • Statistical analysis revealing that for mid-range rare-earth metals up to Er, the RE-Co interactions are predominant, confirming the TbCo2In-type structure as the correct model for ErCo2In [28].
• Implication: Correct site assignment is fundamental, as the crystal structure directly governs material properties, including magnetism and transport behavior [28].

Navigating Analytical Challenges: Troubleshooting Common Issues in Structure Determination

Resolving Overlapping Peaks in Powder X-ray Diffraction Patterns

Overlapping peaks in powder X-ray diffraction (PXRD) present a significant challenge in inorganic crystal structure determination. This phenomenon occurs when multiple Bragg reflections converge at similar diffraction angles, obscuring the individual intensities necessary for determining atomic positions within the unit cell. The problem is particularly acute for materials with low symmetry, complex structures, or nanoscale domains, where peak broadening further compounds the issue. Consequently, resolving these overlaps is a critical step for accurate phase identification, structure solution, and refinement in materials research and drug development. This application note details both established and emerging methodologies for addressing this fundamental analytical hurdle, providing researchers with practical protocols and advanced computational tools to enhance structural insights from PXRD data.

The Challenge of Peak Overlap in PXRD

In powder diffraction, the three-dimensional information contained in single-crystal diffraction is compressed into a one-dimensional pattern, inevitably leading to the overlap of reflections. This loss of information makes determining the correct crystal structure particularly difficult. The intensity of a diffraction peak is governed by the structure factor, which depends on the type and position of atoms within the unit cell. When peaks overlap, their individual intensities become ambiguous, hindering the process of deducing the atomic arrangement. It is estimated that over 476,000 entries in the Powder Diffraction File (PDF) have some unresolved atomic coordinates, underscoring the pervasiveness of this challenge [10].

Traditional approaches to this problem have included the use of global optimization algorithms—such as simulated annealing, genetic algorithms, and particle swarm optimization—to deduce atomic positions. However, these methods often require prior knowledge of the space group and structural units to constrain the number of free parameters. Furthermore, the final Rietveld refinement step is highly sensitive to the initial structural model and typically demands significant expert intervention and intuition to achieve a satisfactory fit [10].

Comparative Methods for Resolving Overlapping Peaks

Table 1: Overview of Techniques for Resolving Overlapping PXRD Peaks

Method Category	Specific Technique	Underlying Principle	Key Application / Advantage	Inherent Limitation
Instrumental & Data Collection	High-Resolution Optics [29]	Uses monochromators to produce pure Cu Kα1 radiation, reducing peak asymmetry.	Provides superior data quality as a foundation for all analysis.	Requires specialized, often costly, instrumentation.
	Fast Data Collection [30]	Employs high-brightness sources & efficient detectors for operando studies.	Captures full XRD spectra in ~10 s; monitors transient phases.	Data quality may be lower than synchrotron sources.
Computational & Traditional Analysis	Rietveld Refinement [29]	Fits a whole-pattern model using a least-squares approach.	Industry standard for final structure refinement.	Requires a good starting model; can be labor-intensive.
	Le Bail & Pawley Fits [29]	Extracts integrated intensities without a structural model.	Useful for initial lattice parameter refinement.	Does not provide atomic coordinates.
	Charge Flipping & Difference Fourier [29]	Direct space methods to deduce atom positions from diffraction data.	Can solve structures ab initio.	Success varies with data quality and complexity.
Artificial Intelligence (AI)	PXRDGen (Diffusion/Flow Models) [10]	Generative AI learns joint structural distributions from stable crystals & their PXRD.	End-to-end structure solution; high accuracy (96% match rate); automates refinement.	Model performance depends on training data diversity.
	Supervised ML for Microstructure [31]	Regression models trained on simulated XRD profiles to predict descriptors.	Predicts pressure, dislocation density, and phase fractions.	Transferability to new materials/orientations can be limited.
	TNEC Classifier for HEAs [32]	Hybrid tree-neural ensemble model for phase classification.	High accuracy (92%) in classifying complex alloy phases.	Requires a large, high-quality, pre-processed dataset.

Detailed Experimental Protocols

Protocol 1: AI-Driven Structure Solution with PXRDGen

PXRDGen represents a transformative, end-to-end neural network for determining crystal structures from PXRD data, effectively addressing peak overlap through data-driven learning [10].

• Sample Preparation & Data Collection: Prepare a pristine powder sample following best practices to minimize preferred orientation and reduce micro-absorption. Load the sample onto a standard powder diffractometer. Collect data over a sufficient 2θ range with an adequate step size and counting statistics to ensure a high signal-to-noise ratio.
• Data Preprocessing: Perform standard data reduction steps on the raw intensity data. This includes subtracting the background and correcting for instrumental effects. The resulting cleaned PXRD pattern is the primary input for the model.
• Structure Generation:
  • Input: Feed the preprocessed PXRD pattern and the known chemical formula of the material into the PXRDGen network.
  • Process: The system utilizes three integrated modules:
    • XRD Encoder (PXE): A pre-trained encoder (based on Transformer or CNN architectures) processes the PXRD pattern into a compact feature vector. This encoder is trained using contrastive learning to align the PXRD data with its corresponding crystal structure in a shared latent space, achieving a top-10 retrieval hit rate of 92.42% for the Transformer-based encoder [10].
    • Crystal Structure Generation (CSG): A conditional generative model (diffusion or flow-based) uses the encoded PXRD features and the chemical formula to generate candidate crystal structures. The model is conditioned to produce structures whose theoretical diffraction pattern matches the input.
    • Cell Parameter Handling: The unit cell parameters can be provided either from conventional indexing software or predicted by an integrated Conditional Cell Generation network (CellNet) within the framework.
• Automated Refinement: The candidate structures generated by the CSG module are automatically passed to the integrated Rietveld refinement (RR) module. This module optimizes the structural parameters to achieve the best possible fit between the calculated pattern of the model and the experimental PXRD data.
• Validation: The final, refined structure is validated by its high match rate with the ground truth (82% for a single sample, 96% for 20 samples on the MP-20 dataset) and a low Root Mean Square Error (RMSE), often less than 0.01, indicating atomic-level accuracy [10].

Protocol 2: Traditional Software-Assisted Ab Initio Structure Solution

For researchers using commercial software suites like HighScore Plus, the workflow for tackling unknown structures with overlapping peaks involves several iterative steps [29].

• Peak Analysis and Indexing:
  • Perform a peak search on the collected PXRD pattern.
  • Use the identified peak positions (2θ values) with the software's indexing algorithms (e.g., in HighScore Plus) to determine the unit cell parameters (a, b, c, α, β, γ). This step may involve real or reciprocal space methods.
• Space Group Determination:
  • Analyze the list of indexed peaks for systematic absences to determine the possible space group.
  • Utilize the software's symmetry explorer to evaluate and select the most probable space group.
• Initial Structure Solution via Direct Methods:
  • With the unit cell and space group known, use integrated direct methods such as Charge Flipping to generate an initial electron density map and deduce the approximate positions of atoms within the unit cell.
• Model Building and Completion:
  • Interpret the electron density map to place atoms. Heavy atoms are typically located first.
  • Use Difference Fourier calculations to locate missing or light atoms that may have been missed in the initial solution.
• Rietveld Refinement:
  • Input the initial structural model into the Rietveld refinement module.
  • Refine the structural parameters (atomic coordinates, site occupancies, thermal displacement parameters) and profile parameters simultaneously to minimize the difference between the observed and calculated patterns. This process requires careful monitoring to ensure physical meaningfulness.

Workflow Diagram: Traditional vs. AI-Driven Approaches

The following diagram illustrates the logical steps and decision points in the two primary workflows for resolving overlapping peaks and determining crystal structures.

Workflow Comparison for PXRD Structure Solution

The Scientist's Toolkit: Essential Research Reagents & Materials

Table 2: Key Materials and Software for PXRD Analysis

Item Name	Type	Critical Function	Application Note
HighScore Plus [29]	Software Suite	Integrated environment for peak analysis, indexing, space group determination, and Rietveld refinement.	Industry-standard platform that incorporates charge flipping and difference Fourier methods for structure solution.
Empyrean Alpha-1 [29]	X-ray Diffractometer	High-resolution instrument with Johansson-type monochromator for pure Cu Kα1 radiation.	Provides the high-quality data essential for resolving subtle overlaps and accurately determining complex structures.
PXRDGen Model [10]	AI Software	End-to-end neural network for solving and refining crystal structures from PXRD in seconds.	Achieves record match rates; particularly effective for locating light atoms and distinguishing neighboring elements.
Ga–In Alloy Metal-Jet X-ray Source [30]	Laboratory X-ray Source	High-brightness source (~3.0×10¹⁰ photons/(s·mm²·mrad²)) for fast data collection.	Enables operando studies (e.g., in batteries) by capturing full spectra in ~10 seconds with synchrotron-like quality.
Soller Slits [33]	Optical Component	Collimates the X-ray beam, reducing axial divergence.	Using smaller slits improves angular resolution at the cost of intensity, helping to separate closely spaced peaks.
SuO-Glu-Val-Cit-PAB-MMAE	SuO-Glu-Val-Cit-PAB-MMAE, MF:C67H103N11O17, MW:1334.6 g/mol	Chemical Reagent	Bench Chemicals

Resolving overlapping peaks in PXRD patterns is a central problem in inorganic crystal structure determination. While traditional software-driven methods provide a robust, well-understood pathway, they often require significant expertise and time. The emergence of powerful AI tools like PXRDGen marks a paradigm shift, offering an automated, rapid, and highly accurate alternative that directly addresses the core issue of peak overlap through data-driven learning. The choice between these methods depends on the specific research goals, available resources, and the complexity of the material system. Ultimately, the continued integration of AI with high-quality experimental data and traditional refinement techniques promises to significantly accelerate the pace of materials discovery and characterization.

Strategies for Locating Light Elements like Hydrogen and Lithium

The accurate determination of crystal structures containing light elements, such as hydrogen and lithium, is a fundamental challenge in inorganic materials research. These elements are pivotal in many modern technologies, including hydrogen storage systems, lithium-ion batteries (LIBs), and superconductors [34]. Their precise localization within a crystal lattice is critical for understanding material properties, guiding the rational design of new compounds, and optimizing performance in applications like drug development and energy storage.

The primary challenge stems from the inherent physical properties of these atoms. With X-rays, the scattering power of an atom is proportional to its electron density. Hydrogen, possessing only a single electron, has a scattering factor less than one-fortieth that of a carbon atom, making it notoriously difficult to detect with conventional X-ray diffraction (XRD) [34]. Similarly, lithium, with just three electrons, also presents a weak signal. This technical difficulty often leaves the positions of hydrogen and lithium atoms unresolved in crystal structures, creating a significant gap in our understanding of structure-property relationships [35] [34].

This Application Note outlines established and emerging strategies to overcome this challenge, focusing on neutron-based techniques and advanced computational methods integrated with X-ray data.

Technical Approaches and Quantitative Comparison

The most effective strategies for locating light elements leverage the complementary strengths of different probes. The table below summarizes the key techniques, their principles, and their applicability.

Table 1: Comparison of Techniques for Locating Light Elements

Technique	Fundamental Principle	Sensitivity for Light Elements	Key Applications	Primary Limitations
X-ray Diffraction (XRD)	Scattering of X-rays by atomic electrons [36].	Low (proportional to electron count); challenging for H/Li [34].	Standard crystallography; phase identification [36].	Weak scattering signal from H (1 electron) and Li (3 electrons) [34].
Neutron Diffraction	Scattering of neutrons by atomic nuclei [37] [34].	High; independent of electron count; excellent for H, Li [37] [34].	Precise location of H/Li in metal hydrides, battery materials, and amino acids [34].	Requires large-scale facilities (reactors/accelerators); limited availability [34].
Total Scattering with Neutrons	Analyzes both Bragg and diffuse scattering from neutrons [34].	High for H/Li; probes average local structure, including disordered atoms.	Studying disordered structures, liquids, and local H environments [34].	Complex data analysis; requires specialized instruments like NOVA at J-PARC [34].
AI-Enhanced Powder XRD (e.g., PXRDGen)	Neural networks learn joint structural distributions from crystals and their PXRD data [27] [35].	High accuracy in locating light atoms and differentiating neighboring elements from PXRD data [27] [35].	Automated crystal structure determination from powder samples, including H/Li positioning [35].	Model performance dependent on training data; a developing field.

The selection of an appropriate technique depends on the specific research question, sample availability, and access to facilities. Neutron diffraction remains the gold standard for direct, experimental observation of light elements, while AI-enhanced methods offer a powerful, accessible complement for high-throughput analysis.

Experimental Protocols

Protocol: Locating Light Elements Using Neutron Diffraction

This protocol details the procedure for determining the crystal structure of a material containing light elements using a high-intensity neutron diffractometer, such as the NOVA beamline at J-PARC [34].

1. Sample Preparation

• Material: The sample must be synthesized in a sufficient quantity (from milligrams to grams, depending on the instrument's sensitivity) [34].
• Containment: Load the powdered or solid sample into a suitable container (e.g., a vanadium can or a quartz capillary) that exhibits minimal neutron scattering and absorption.
• Special Atmosphere: For air-sensitive materials or studies under gas atmospheres (e.g., hydrogen), use specialized sample cells that allow for controlled gas loading and sealing [34].

2. Data Collection

• Instrument Setup: Mount the sample on the diffractometer. Instruments like NOVA have multiple detectors arranged three-dimensionally to capture neutrons scattered in all directions [34].
• Measurement Parameters: Set the incident neutron wavelength, and define the measurement duration based on the required statistical accuracy and temporal resolution for in situ or operando studies [38].
• Data Acquisition: Expose the sample to the neutron beam and collect the diffraction patterns. For time-resolved studies, collect sequential datasets to track structural evolution, such as lithium movement during battery charging/discharging [38] [34].

3. Data Analysis

• Unit Cell Determination: Index the diffraction pattern to determine the unit cell parameters using standard software.
• Structure Solution: Use direct methods or charge-flipping techniques to obtain an initial structural model.
• Rietveld Refinement: Refine the crystal structure model against the entire neutron diffraction pattern. The strong scattering signal from hydrogen and lithium nuclei will allow for accurate refinement of their atomic coordinates, occupancy, and thermal parameters [34].

Protocol: AI-Augmented Structure Determination from Powder XRD

For situations where neutron sources are inaccessible, PXRDGen provides an AI-driven method to determine structures, including the positions of light atoms, from conventional powder XRD data [35].

1. Data Input

• PXRD Pattern: Input the experimental powder X-ray diffraction pattern of the sample.
• Chemical Formula: Provide the known chemical formula of the compound.

2. AI-Powered Structure Solution with PXRDGen

• XRD Encoder: A pre-trained neural network module (using Contrastive Learning) extracts structural features from the PXRD pattern, creating a latent representation that guides structure generation [35].
• Crystal Structure Generation (CSG): A conditional generative model (diffusion or flow-based) produces candidate crystal structures. This model is conditioned on the features from the XRD encoder and the chemical formula [35].
• Unit Cell Handling: The unit cell parameters can be provided from conventional indexing of the PXRD data or predicted by an integrated Conditional Cell Generation network (CellNet) [35].

3. Validation and Refinement

• Rietveld Refinement (RR) Module: The top candidate structures generated by the CSG module are automatically refined using Rietveld refinement against the experimental PXRD data to ensure optimal agreement [35].
• Output: The final output is an atomically accurate crystal structure, with the positions of light elements like hydrogen and lithium resolved [35].

The workflow for this AI-augmented method is illustrated below:

The Scientist's Toolkit: Essential Research Reagents and Materials

Successful experimental analysis of light elements requires specific materials and reagents. The following table details key items used in the featured protocols.

Table 2: Essential Research Reagents and Materials

Item	Function / Application	Critical Specifications
Deuterated Compounds	Replaces hydrogen with deuterium in samples for neutron studies; deuterium has a different, often more favorable, neutron scattering cross-section.	Isotopic purity >99%.
Vanadium Sample Can	A common sample holder for neutron diffraction; vanadium has a negligible coherent neutron scattering cross-section, minimizing background.	High purity; specific wall thickness for sample volume and pressure containment.
Specialized Electrolytes	For operando studies of lithium-ion batteries, enabling the tracking of lithium diffusion during cycling [38].	Lithium salt (e.g., LiPF₆) in organic solvents (e.g., ethylene carbonate/dimethyl carbonate) [39].
High-Pressure Cells	Allows for neutron diffraction experiments under ultrahigh pressure to study changes in properties and hydrogen positions under extreme conditions [34].	Material strength (e.g., diamond anvils); pressure calibration.
Reference Crystal Standards	Used for instrument calibration and validation of the structure determination process (e.g., NIST standard reference materials).	Well-characterized crystal structure with known lattice parameters.

Concluding Remarks

The strategic localization of light elements is no longer an insurmountable challenge. Neutron diffraction, particularly at high-intensity facilities like J-PARC, provides an unambiguous, direct method for pinpointing hydrogen and lithium [34]. The correlative use of X-ray and neutron tomography offers a powerful multi-modal approach, combining the high-resolution structural information from X-rays with the lithium-sensitive contrast from neutrons [38]. Furthermore, the emergence of sophisticated AI tools like PXRDGen represents a paradigm shift, enabling the resolution of light atoms from standard powder XRD data with unprecedented speed and accuracy [35]. By integrating these advanced strategies, researchers can fully elucidate inorganic crystal structures, accelerating the development of next-generation functional materials.

Addressing Limitations of Sample Quality and Crystal Size

A primary challenge in inorganic crystal structure determination is obtaining single crystals of sufficient size and quality for conventional single-crystal X-ray diffraction (SCXRD). Many advanced materials, including complex metal-organic frameworks (MOFs), catalysts, and nanocomposites, naturally form as microcrystalline powders or nanocrystals that are resistant to growth into larger single crystals [10] [40]. This application note details contemporary methodologies and protocols designed to overcome these limitations, enabling high-resolution structural analysis from sub-optimal samples. These approaches are critical for researchers in materials science and chemistry to characterize novel compounds that defy traditional crystallographic analysis.

Advanced Methodologies for Small and Imperfect Crystals

When single crystals larger than several microns are unavailable, researchers can employ alternative techniques. The table below summarizes the key modern methods for handling such challenging samples.

Table 1: Modern Techniques for Crystal Structure Determination from Challenging Samples

Technique	Principle	Ideal Crystal Size	Key Application	Reported Resolution
Serial Femtosecond Crystallography (SFX)	"Diffraction-before-destruction" using ultrafast X-ray pulses from an X-ray Free-Electron Laser (XFEL) to probe microcrystals [41] [40].	Nanocrystals to microns [40]	Radiation-sensitive materials, room-temperature studies, nanocrystals [40].	Atomic (e.g., Lysozyme at 1.9 Ã… [41])
Powder X-ray Diffraction (PXRD) with AI	End-to-end neural networks (e.g., PXRDGen) solve and refine structures from one-dimensional powder diffraction patterns [10].	Polycrystalline powder	Materials only available as powders; automated structure solution [10].	Atomic (RMSE < 0.01 vs. ground truth [10])
Small-Molecule Serial Femtosecond Crystallography (smSFX)	A specialized form of SFX using graph theory algorithms to analyze weak diffraction patterns from very small molecules [40].	~5 microns or less [40]	Identifying architecture of unknown molecular structures from nanocrystals [40].	Successfully determined structures of thiorene and tethrene [40]

Experimental Protocols

Protocol: Small-Molecule Serial Femtosecond Crystallography (smSFX)

This protocol is adapted for inorganic nanocrystals, based on the methodology that successfully determined the structures of mithrene, thiorene, and tethrene [40].

1. Sample Preparation

• Synthesis & Harvesting: Synthesize the target inorganic nanocrystals. Harvest the resulting microcrystalline or nanocrystalline powder.
• Suspension: Suspend the nanocrystals in a suitable inert mother liquor or solvent to prevent dissolution or reaction. The suspension must be homogeneous to ensure consistent delivery.
• Loading: Load the crystal suspension into the reservoir of a liquid injection system, such as a gas dynamic virtual nozzle (GDVN) jet or a high-viscosity extruder.

2. Data Collection at an XFEL

• Instrument: Perform the experiment at an XFEL facility, such as the Linac Coherent Light Source (LCLS).
• Crystal Delivery: Inject the crystal suspension across the path of the XFEL beam in a continuous stream. The jet diameter is typically on the order of one micron [40].
• Data Acquisition: Fire femtosecond (one quadrillionth of a second) X-ray pulses at the stream [40]. Each pulse diffracts from a single nanocrystal and is destroyed, but the diffraction pattern is captured by a detector before the destruction occurs. Collect tens to hundreds of thousands of these "single-shot" diffraction patterns.

3. Data Processing and Analysis

• Real-Time Transfer: Use a high-speed network (e.g., ESnet) to transfer the terabytes of data generated to a high-performance computing (HPC) center for immediate processing [40].
• Indexing and Integration: Use specialized algorithms (e.g., a graph theory-based algorithm [40]) to index the sparse diffraction patterns from individual nanocrystals.
• Structure Solution: Merge the indexed patterns into a complete 3D diffraction dataset. Solve the crystal structure using direct methods or other phasing approaches suitable for small molecules.

The following workflow diagram outlines the key steps in the smSFX process:

Protocol: AI-Augmented Powder X-ray Diffraction (PXRD)

For polycrystalline samples, PXRD can be used for structure determination when combined with modern AI-driven software like PXRDGen [10].

1. Data Collection

• Sample Loading: Fill a standard capillary or a flat sample holder with the homogeneous polycrystalline powder of the inorganic material.
• Diffraction Measurement: Place the sample in a laboratory X-ray diffractometer or synchrotron beamline. Collect a high-quality PXRD pattern over a sufficient 2θ range (e.g., 5-80° or higher) with good counting statistics.

2. AI-Driven Structure Solution with PXRDGen

• Unit Cell Determination: Use conventional auto-indexing software to determine the unit cell parameters from the PXRD pattern.
• Structure Generation: Input the chemical formula and the PXRD data into the PXRDGen neural network. The network, which integrates a pre-trained XRD encoder and a crystal structure generator, will produce multiple candidate atomic structures [10].
• Validation and Refinement: The integrated Rietveld refinement module automatically refines the best candidate structure(s) against the experimental PXRD data. The final structure should show excellent agreement (low Rwp and Rp values) with the experimental pattern.

Table 2: Key Research Reagent Solutions for Sample Preparation

Reagent / Material	Function in Protocol	Example Application
High-Viscosity Extruder (HVE)	Delivers a stream of microcrystals suspended in a viscous matrix (e.g., lipidic cubic phase) to the X-ray beam, dramatically reducing sample consumption [41] [42].	Delivery of thermolysin, glucose isomerase, and other standard protein microcrystals [42].
Liquid Injection System	Creates a thin liquid jet containing the crystal suspension, allowing for rapid sample replenishment for each XFEL pulse [41].	Standard method for SFX experiments on proteins like lysozyme and photosystem I [41] [42].
Fixed-Target Chips	Microfluidic chips or grids that hold thousands of crystals in known locations. The chip is raster-scanned through the X-ray beam, minimizing sample waste [41].	Used with proteinase K and lysozyme for serial synchrotron crystallography (SSX) [42].

The Scientist's Toolkit

The following workflow illustrates the integrated process of AI-augmented PXRD, from data collection to final refined structure:

Optimizing Data Collection and Computational Workflows for Efficiency

The determination of inorganic crystal structures is a cornerstone of materials science, chemistry, and drug development. Traditional methods for solving crystal structures from X-ray diffraction data, while powerful, are often labor-intensive, time-consuming, and require significant expertise. Recent advances in both data collection protocols and computational workflows are revolutionizing this field, enabling faster, more accurate, and more efficient structure determination. This application note details optimized methodologies for inorganic crystal structure determination, focusing on integrated approaches that combine rigorous experimental practices with state-of-the-art computational algorithms, including machine learning and multi-objective evolutionary searches.

Optimized Experimental Data Collection Protocols

High-quality data collection forms the foundation for successful crystal structure determination. The following protocols summarize best practices for powder X-ray diffraction (PXRD) data collection, specifically tailored for inorganic materials.

Instrument Configuration and Setup

Table 1: Recommended Instrument Configuration for PXRD Data Collection

Parameter	Recommended Specification	Rationale
Incident Wavelength	Monochromatic Cu Kα1 (λ = 1.54056 Å)	Stronger diffraction intensity (∝ λ³) compared to Mo radiation; eliminates need for computational line stripping [43].
Geometry	Capillary transmission (0.7 mm diameter)	Minimizes preferred orientation effects; ensures optimal beam-sample interaction [43].
Particle Size	20–50 μm	Balances homogeneous packing, true powder average, and mitigation of preferred orientation [43].
Detector Type	Position-sensitive detector with energy discrimination	Superior resolution and count rates; suppresses fluorescence from organometallic samples [43].
Temperature Control	~150 K (open-flow N₂ gas cooler)	Improves signal-to-noise at high 2θ values; mitigates form-factor fall-off [43].

Data Collection Strategies

Table 2: Data Collection Schemes for Different Stages of SDPD

Purpose	Time	Count Type	Range (°2θ)	Resolution (Å)	Step Size (°)
Indexing, Pawley refinement, global optimization	2 hours	Fixed	2.5–40	2.25	0.017 [43]
Rietveld refinement	12 hours	Variable (VCT)	2.5–70	1.35	0.017 [43]

Variable Count Time (VCT) Scheme: 2.5–22° (2s/step); 22–40° (4s/step); 40–55° (15s/step); 55–70° (24s/step) [43]. This ensures adequate signal-to-noise at high angles where diffraction intensity is weak but critical for accurate refinement.

Computational Workflows for Enhanced Efficiency

AI-Driven Structure Determination

Recent breakthroughs in artificial intelligence have dramatically accelerated crystal structure determination from PXRD data. The PXRDGen framework represents a significant advancement in this area.

Table 3: Performance Metrics of AI-Based Structure Determination Models

Model	Dataset	Key Components	1-Sample Match Rate	20-Sample Match Rate	RMSE
PXRDGen	MP-20 (inorganic)	Pretrained XRD encoder, diffusion/flow-based generator, Rietveld refinement	82%	96%	<0.01 [10]
XDXD	COD (24,000 structures)	Transformer-based XRD encoder, diffusion-based generator	70.4% (at 2.0 Ã… resolution)	N/A	<0.05 [9]

PXRDGen integrates three specialized modules: (1) a pre-trained XRD encoder using contrastive learning to align PXRD patterns with crystal structures; (2) a crystal structure generation module based on diffusion or flow models conditioned on PXRD features and chemical formulas; and (3) an automated Rietveld refinement module that ensures optimal alignment between predicted structures and experimental data [10]. This integrated approach effectively addresses key challenges in PXRD analysis, including resolution of overlapping peaks, localization of light atoms, and differentiation of neighboring elements.

For single-crystal data at low resolution, the XDXD framework provides an end-to-end solution that predicts complete atomic models directly from diffraction data, bypassing the need for manual interpretation of ambiguous electron density maps [9].

Computational-Experimental Hybrid Approaches

Evolutionary algorithms enhanced with experimental data offer another powerful approach for structure determination. The XtalOpt-VC-GPWDF method combines multi-objective evolutionary searches with experimental PXRD pattern matching:

Diagram 1: PXRD-assisted evolutionary algorithm workflow for crystal structure prediction.

The fitness function combines both enthalpy (H) and PXRD similarity (S):

where w is the weight assigned to the PXRD similarity objective [44]. This approach transcends limitations of both computational methods (e.g., 0 K approximation) and experimental conditions (e.g., metastability, external stimuli) by searching for structures that simultaneously minimize enthalpy and maximize similarity to experimental data.

Quantum Crystallographic Refinement

For final structure refinement, quantum crystallographic protocols enable exceptionally accurate structure determination, achieving accuracy comparable to neutron diffraction even from X-ray data [45]. Key methods include:

• Hirshfeld Atom Refinement (HAR): Provides accurate hydrogen atom positions and displacement parameters, effective even at standard Cu Kα resolution limits [45].
• X-ray Constrained Wavefunction (XCW) Fitting: Derives experimental wavefunctions related to chemical bonding and materials properties [45].
• Multipole Model (MM): Traditional charge-density analysis that accounts for non-spherical electron density distributions [45].

A standardized Quantum Crystallographic Protocol (QCP) has been developed for general use, making these advanced refinement techniques accessible for routine structure determination [45].

The Scientist's Toolkit: Essential Research Reagents and Software

Table 4: Key Research Reagent Solutions for Efficient Crystal Structure Determination

Tool/Category	Specific Examples	Function/Application
Structure Solution Software	DASH, MDASH, GALLOP	Indexing, space-group determination, crystal structure solution from PXRD data [43]
Refinement Packages	TOPAS-Academic, ShelXL, Tonto	Rietveld refinement, Hirshfeld Atom Refinement, multipole refinement [43] [45]
Quantum Crystallography	Tonto, NoSpherA2, XD	Advanced refinement using non-spherical scattering factors; accurate H-atom positioning [45]
DFT Optimization	VASP, ORCA, Quantum ESPRESSO	Geometry optimization of crystal structures; energy calculations [43] [44]
Validation Tools	Mogul, PLATON	Molecular geometry validation; crystal structure validation [43]
Crystallographic Databases	Cambridge Structural Database (CSD), Crystallography Open Database (COD)	Primary sources of crystal structure data for comparison and machine learning training [43] [9]
Data Collection Hardware	Borosilicate glass capillaries (0.7 mm), Open-flow Nâ‚‚ cryocoolers	Sample containment for transmission geometry; temperature control for improved data quality [43]

Integrated Workflow for Efficient Structure Determination

Diagram 2: Integrated end-to-end workflow for efficient crystal structure determination.

This optimized workflow integrates the best practices outlined in this document:

• Sample Preparation and Data Collection: Following the protocols in Section 2 ensures high-quality input data.
• Initial Processing: Standard indexing and Pawley refinement prepare data for structure solution.
• AI-Driven or Evolutionary Structure Solution: Depending on data type and quality, employ either end-to-end neural networks (PXRDGen for powders, XDXD for single crystals) or evolutionary approaches enhanced with experimental data.
• Quantum Crystallographic Refinement: Apply advanced refinement techniques to achieve maximum accuracy, particularly for light atom positioning and electron density analysis.
• Validation: Final validation using established tools ensures structural reliability and geometric sensibility.

The integration of optimized experimental protocols with advanced computational workflows represents a paradigm shift in inorganic crystal structure determination. The methodologies detailed in this application note—including AI-driven structure solution, evolutionary algorithms guided by experimental data, and quantum crystallographic refinement—collectively enable researchers to achieve unprecedented efficiency and accuracy in structure determination. By adopting these integrated approaches, research teams can significantly accelerate materials characterization and drug development processes while maintaining the highest standards of structural accuracy.

Ensuring Accuracy: Validation Protocols and Comparative Technique Analysis

This application note provides a comprehensive guide to the essential validation metrics utilized in the determination of inorganic and macromolecular crystal structures via X-ray diffraction. We detail the experimental protocols and quantitative assessment criteria for R-factors, Root-Mean-Square-Error (RMSE/RMSD) of stereochemical parameters, and the Ramachandran plot—a cornerstone of protein backbone validation. While the principles of R-factors and RMSD are universally applicable across crystallography, the Ramachandran plot is specific to the validation of polypeptide chains. The note is structured to equip researchers and drug development professionals with the methodologies to rigorously assess the quality and reliability of their crystallographic models, thereby ensuring the integrity of structural data used in downstream applications such as rational drug design.

In X-ray crystallography, a refined atomic model is an interpretation of the experimental electron density map. Validation is the critical process of assessing how well this model agrees with both the experimental data and established stereochemical rules [46] [47]. For inorganic crystal structures and small molecules, this primarily involves agreement with diffraction data and known bond geometry. For macromolecules like proteins, the validation process is more complex due to their larger size, lower resolution data, and intricate polymeric structure. Key metrics have been developed to provide objective measures of a model's quality, falling into two primary categories: experimental fit metrics, which assess how well the model explains the collected X-ray data (e.g., R-factors), and stereochemical or geometric quality metrics, which assess how well the model conforms to ideal chemical geometry (e.g., RMSD and the Ramachandran plot) [46] [48]. The worldwide Protein Data Bank (PDB) has established validation as a mandatory step for deposition, emphasizing its importance to the scientific community [49].

Core Validation Metrics: Definitions and Protocols

R-factors: Assessing Agreement with Experimental Data

Definition and Mathematical Formulation

The R-factor (also known as the residual factor, reliability factor, or R-work) is a primary indicator of the agreement between the atomic model and the experimental X-ray diffraction data [50] [51]. It is defined by the equation:

$$R = \frac{\sum ||F{\text{obs}}| - |F{\text{calc}}||}{\sum |F_{\text{obs}}|}$$

where $F{\text{obs}}$ is the observed structure factor amplitude from the diffraction experiment, and $F{\text{calc}}$ is the structure factor amplitude calculated from the atomic model [50]. The sum extends over all measured reflections. The R-factor measures the average disagreement between the model and the data; a value of 0 indicates perfect agreement, while higher values indicate poorer agreement.

The Free R-factor (R-free)

To prevent overfitting during refinement, a subset of reflections (typically 5-10%) is excluded from the refinement process. The R-free is then calculated using only this excluded set [50]. This provides an unbiased estimate of the model's quality and its ability to predict new data. A significant discrepancy between R-work and R-free can indicate over-fitting, where the model has been tailored too specifically to the refinement data at the expense of predictive accuracy.

Experimental Protocol and Interpretation

The protocol for calculating R-factors is integrated into the structure refinement process. The following workflow is standard:

• Refinement Cycle: The atomic model parameters (coordinates, B-factors) are adjusted to minimize the difference between $|F{\text{calc}}|$ and $|F{\text{obs}}|$, typically by minimizing a least-squares target.
• Calculation: After each refinement cycle, both R-work and R-free are calculated.
• Monitoring: The convergence of R-work and R-free is monitored. Refinement is considered complete when these values stabilize and can no longer be improved significantly.

Table 1: Typical R-factor Values in Crystallography [51] [48]

Structure Type	Typical R-work/R-free Range	Interpretation
Small Molecule / Inorganic	~0.04 - 0.05	Near-experimental error
High-Resolution Protein (<1.5 Ã…)	~0.15 - 0.20	Excellent agreement
Medium-Resolution Protein (~2.0 Ã…)	~0.18 - 0.23	Good agreement
Lower-Resolution Protein (>2.5 Ã…)	~0.20 - 0.30	Caution advised; requires careful validation

Root-Mean-Square-Error (RMSE/RMSD) of Stereochemistry

Definition and Mathematical Formulation

In crystallographic validation, the Root-Mean-Square-Error (RMSE) or Root-Mean-Square Deviation (RMSD) measures the average deviation of a model's geometric parameters, such as bond lengths and bond angles, from ideal or target values established from high-resolution small-molecule structures [46] [52]. The RMSD for a set of parameters is defined as:

$$\text{RMSD} = \sqrt{\frac{\sum{i=1}^{n}(X{i,\text{model}} - X_{i,\text{target}})^2}{n}}$$

where $X{i,\text{model}}$ is the value of the parameter (e.g., a specific C-C bond length) in the refined model, $X{i,\text{target}}$ is the ideal library value for that parameter, and $n$ is the number of such parameters [52].

Experimental Protocol and Interpretation

Stereochemical RMSD is not a direct result of the experiment but is a product of the refinement process using stereochemical restraints.

• Restraint Application: During refinement, the model's bond lengths and angles are restrained to stay near ideal values found in stereochemical libraries (e.g., the Engh & Huber library for proteins) [46]. This is necessary because the experimental data alone is often insufficient to define all atomic positions with high precision.
• Library Comparison: Upon refinement completion, software tools (e.g., MolProbity, PROCHECK) calculate the RMSD for bond lengths and angles by comparing the final model to the restraint library.
• Quality Assessment: A low RMSD indicates that the model's geometry is consistent with well-established chemical knowledge.

Table 2: Target Values for Stereochemical RMSD in Protein Structures [46]

Geometric Parameter	Target RMSD Value	Interpretation
Bond Lengths	~0.02 Ã…	Ideal value, corresponds to uncertainty of targets themselves
Bond Angles	0.5° - 2.0°	Expected range for a well-refined model
Excessively Low RMSD	Significantly below 0.02 Ã…	May indicate an over-restrained, overly idealized model
Excessively High RMSD	> ~0.03 Ã… for bonds	Suggests potential problems with the model or refinement

The Ramachandran Plot: Validating Protein Backbone Torsion

Definition and Theoretical Basis

The Ramachandran plot is a fundamental validation tool for protein structures, assessing the plausibility of the backbone conformation by plotting the phi (φ) and psi (ψ) torsion angles of all non-glycine, non-proline amino acid residues [46] [53]. These angles define the rotation of the polypeptide chain around the N-Cα and Cα-C bonds, respectively. Due to steric clashes between atoms of the backbone and side chains, only certain combinations of φ and ψ are sterically allowed [53]. The plot is divided into "core" (most favored), "allowed," "generously allowed," and "disallowed" regions. Glycine residues, which lack a side chain, have greater conformational freedom and are analyzed on a separate plot.

Experimental Protocol for Analysis

The analysis is performed automatically by validation software post-refinement.

• Data Extraction: The φ and ψ angles for each residue are calculated from the atomic coordinates of the final model.
• Plotting and Calculation: Software (e.g., MolProbity, PROCHECK, PHENIX) plots these angles and calculates the percentage of residues in each region of the Ramachandran plot.
• Outlier Identification: Residues falling in the "disallowed" regions are flagged as outliers and require careful inspection.

Interpretation and Quality Thresholds

For a high-quality protein structure, expectations are high:

• >98% of non-glycine/non-proline residues should be in the allowed regions [46].
• >90% of residues are typically found in the most favored regions for a well-refined model at good resolution [48]. The presence of outliers does not automatically invalidate a structure, but each must be justified by clear, unambiguous electron density. A cluster of outliers may indicate a more significant problem with the model.

The Scientist's Toolkit: Essential Research Reagents and Software

This section details the key computational tools and resources required for effective crystallographic validation.

Table 3: Essential Software Tools for Crystallographic Validation

Tool Name	Type/Function	Key Use in Validation
MolProbity [47] [48]	Validation Server/Suite	All-atom contact analysis, steric clashes, Ramachandran plots, and rotamer outliers.
PROCHECK [47] [48]	Validation Software	Detailed stereochemical analysis, including Ramachandran plot quality and overall geometry.
PHENIX [46] [47]	Refinement Suite	Integrated refinement and validation, with tools for comprehensive model quality assessment.
CCP4	Program Suite	Includes multiple utilities for structure solution, refinement, and validation.
Coot [47]	Model Building Tool	Interactive model building and real-time validation, including MolProbity integration.
Cambridge Structural Database (CSD) [46] [47]	Reference Database	Source of ideal small-molecule geometries for creating stereochemical restraint libraries.

Integrated Validation Workflow

A robust validation protocol requires the integrated use of all key metrics. The following diagram illustrates the logical workflow and relationships between these metrics in a typical structure determination pipeline.

The rigorous application of R-factors, RMSD, and the Ramachandran plot is non-negotiable for establishing the credibility of a crystallographic model. R-factors validate the model against the raw experimental data, RMSD ensures its stereochemical rationality, and the Ramachandran plot provides a powerful, restraint-independent check of protein backbone geometry. For researchers in drug development, where structural models directly inform inhibitor design and optimization, adherence to the quality thresholds outlined in this note is paramount. By following the detailed protocols and utilizing the recommended toolkit, scientists can confidently produce and evaluate structural data that is both accurate and reliable, forming a solid foundation for scientific discovery and innovation.

Validation is a critical step in structural biology, ensuring the reliability and accuracy of three-dimensional atomic models. For researchers determining inorganic crystal structures via X-ray diffraction, robust validation protocols are indispensable for assessing model quality, identifying potential errors, and providing confidence in downstream structural analysis. This Application Note provides detailed methodologies for employing three cornerstone validation resources—MolProbity, PROCHECK, and the wwPDB Validation Server—within the context of a structural research workflow. Adherence to the protocols outlined herein will empower researchers to critically evaluate their models, improve structural quality, and produce results that meet the rigorous standards required for publication and deposition in the Protein Data Bank.

Table 1: Overview of Featured Validation Tools

Tool Name	Primary Function	Key Metrics	Access Method
MolProbity	All-atom contact analysis & modern geometry validation	Clashscore, Ramachandran outliers, Rotamer outliers, Cβ deviations [54]	Web server, Stand-alone, Integrated in PHENIX [54]
PROCHECK	Stereochemical quality analysis	Ramachandran plot quality, backbone & sidechain parameters [55]	Web server, Stand-alone
wwPDB Validation Server	Pre-deposition assessment against wwPDB standards	Global quality sliders, geometry outliers, data-model fit (RSRZ), ligand validation [56] [57]	Web server (validate.wwpdb.org)

A successful validation experiment requires access to both the atomic coordinates and the underlying experimental data. The following table lists key reagents and computational tools essential for performing a comprehensive structural validation.

Table 2: Research Reagent Solutions for Structure Validation

Reagent / Resource	Function / Description	Source / Availability
Atomic Coordinate File	The structural model to be validated, typically in PDB or mmCIF format.	Output from refinement programs (e.g., PHENIX, REFMAC5).
Structure Factor File	Experimental data (amplitudes & phases) required for assessing model-to-data fit.	Output from data integration and phasing (e.g., .mtz file).
MolProbity Web Server	Provides all-atom contact analysis and updated geometry criteria [54].	http://molprobity.biochem.duke.edu
wwPDB Validation Server	Produces official pre-deposition validation reports [56].	https://validate.wwpdb.org
Coot Visualization Software	Used for interactive model inspection and correction of validation outliers.	https://www2.mrc-lmb.cam.ac.uk/personal/pemsley/coot/
PHENIX Software Suite	Integrated refinement and validation environment incorporating MolProbity [54].	https://phenix-online.org

Tool-Specific Application Notes and Protocols

MolProbity

Background Principle: MolProbity is a comprehensive structure-validation system that employs modern, all-atom contact analysis, including hydrogen atoms, to identify steric clashes, suboptimal rotamer placements, and backbone conformation errors [54]. Its unique clashscore metric, defined as the number of serious steric overlaps ≥0.4Å per thousand atoms, provides a highly sensitive indicator of local fitting problems [54]. Its criteria are continuously updated using high-quality reference datasets like the Top8000, ensuring robust and contemporary statistical standards [54].

Experimental Protocol:

• Input Preparation: Ensure your input coordinate file is in PDB or mmCIF format. Hydrogen atoms should be added and optimized; the MolProbity server can execute the Reduce tool to add and optimize hydrogens if they are missing.
• Submission: Access the MolProbity website (http://molprobity.biochem.duke.edu) and upload your coordinate file. If available, provide a structure factor file for electron density analysis.
• Analysis: The server will run a suite of validation checks. Upon completion, review the summary page, which highlights key scores like Clashscore, Ramachandran outliers, and Rotamer outliers.
• Outlier Inspection and Correction: Use the interactive visualization in KiNG (for legacy Java) or the provided links to open your structure in Coot. Navigate to each flagged outlier. For rotamer outliers, use Coot's rotamer fitting tools. For clash outliers, manually adjust sidechain or backbone conformations to resolve severe steric overlaps.
• Iterative Refinement: After making corrections in Coot, re-refine the adjusted model in your chosen refinement software (e.g., PHENIX.refine). Repeat the MolProbity validation to ensure improvements and check for new outliers.

PROCHECK

Background Principle: PROCHECK is one of the pioneering validation tools that assesses the stereochemical quality of a protein structure by analyzing residue-by-residue geometry and overall structure geometry [55]. Its most recognized output is the Ramachandran plot, which evaluates the conformational sanity of protein backbone torsion angles (phi and psi) by comparing them to statistically favored regions derived from high-quality structures.

Experimental Protocol:

• Input Preparation: Prepare your coordinate file in standard PDB format.
• Submission and Execution: Access a PROCHECK web server (e.g., via the PDB or EBI) or run the stand-alone program. Upload or specify the path to your coordinate file.
• Report Interpretation: Analyze the generated PostScript output. The key document is the Ramachandran plot summary. A high-quality model is expected to have >90% of residues in the most favored regions. Give particular attention to residues in the disallowed regions.
• Correction of Outliers: For each Ramachandran outlier identified, inspect the residue's fit to the electron density in Coot. If the density supports an alternative conformation, manually adjust the backbone torsion angles to place the residue in an allowed region. Re-refit the surrounding atoms as necessary.

wwPDB Validation Server

Background Principle: The wwPDB Validation Server is the official tool used by the worldwide PDB to generate validation reports during deposition [56]. It integrates community-recommended standards from expert Validation Task Forces and provides a holistic assessment encompassing model geometry, fit to experimental data, and ligand quality [56] [57]. Its "slider" metrics offer a percentile-based comparison of your structure against all entries in the PDB archive.

Experimental Protocol:

• Input Preparation: Gather your final coordinate file (PDB or mmCIF) and the corresponding structure factor file (.mtz or .cif).
• Pre-Deposition Submission: Navigate to the standalone wwPDB Validation Server (https://validate.wwpdb.org). Upload both your coordinate and structure factor files. This step is strongly recommended before formal deposition to identify and rectify issues.
• Report Analysis: Download and scrutinize the comprehensive PDF validation report.
  • Executive Summary: Examine the five key slider metrics: Rfree, Clashscore, Ramachandran outliers, Rotamer outliers, and RSRZ outliers. Aim for all sliders to be in the blue (favorable) percentile zones [57].
  • Outlier Lists: Review the detailed lists of steric clashes, Ramachandran outliers, and rotamer outliers. Cross-reference these with the "Model vs. Data" section to identify residues with poor fit to the electron density.
  • Ligand Validation: For structures with inorganic cofactors or small molecules, check the ligand geometry and fit-to-density metrics. The Mogul Z-scores and Real Space Correlation Coefficient (RSCC) are critical for validating ligand geometry and placement [57].
• Corrective Action: Use the outlier information to guide final model adjustments in Coot and subsequent re-refinement. The goal is to resolve all major geometric and steric issues while maintaining or improving the fit to the experimental data.

Integrated Validation Workflow

A robust validation strategy involves the sequential and iterative use of these tools. The diagram below outlines a logical workflow that integrates MolProbity, PROCHECK, and the wwPDB Validation Server to ensure a thorough assessment.

Integrated Structure Validation Workflow

The consistent application of the validation tools and protocols described in this document—MolProbity for all-atom contacts, PROCHECK for foundational stereochemistry, and the wwPDB Validation Server for a final pre-deposition audit—is fundamental to producing high-quality, reliable inorganic crystal structures. By integrating these validation steps iteratively within the structure determination pipeline, researchers can systematically identify and correct model errors, thereby strengthening the structural conclusions drawn from their research and enhancing the integrity of the public structural data archive.

The determination of inorganic crystal structures from X-ray diffraction (XRD) data is fundamental to advancements in materials science, chemistry, and drug development. Traditional methods for structure determination, particularly from powder X-ray diffraction (PXRD) data, are often labor-intensive, time-consuming, and require significant expert intervention [10]. The inherent challenge of compressing three-dimensional crystal information into a one-dimensional PXRD pattern, coupled with frequent peak overlaps, creates ambiguity that complicates unambiguous structure solution [58].

Recently, artificial intelligence (AI) has emerged as a transformative tool to overcome these challenges. Deep learning models, including graph neural networks, diffusion models, and transformer-based architectures, are now being applied to directly predict crystal structures from diffraction data [9] [10]. Benchmarking the performance of these models through quantitative metrics such as match rates and Root Mean Square Error (RMSE) is essential for evaluating their accuracy, reliability, and potential for automation in research pipelines. This application note provides a structured overview of the current performance benchmarks of state-of-the-art AI models and details the experimental protocols for their evaluation.

Performance Benchmarks of AI Models for Crystal Structure Determination

The performance of AI models is primarily quantified using the match rate, which indicates the percentage of predicted structures that correctly identify the ground-truth crystal structure, and the RMSE, which measures the average deviation of predicted atomic coordinates from their true positions. The following tables consolidate recent benchmark results.

Table 1: Overall Model Performance on Key Datasets

Model Name	Dataset	Key Performance Metrics	Reported Performance
PXRDGen [10]	MP-20 (Inorganic)	Match Rate (1-sample)	82%
		Match Rate (20-sample)	96%
		Root Mean Square Error (RMSE)	< 0.01
XDXD [9]	COD (24,000 structures)	Match Rate (for systems with 0-40 atoms)	~70%
		Match Rate (for systems with 160-200 atoms)	~40%
		Root Mean Square Error (RMSE)	Increases with atom count
Computer Vision Models (e.g., Swin Transformer) [58]	SIMPOD (Space Group Prediction)	Top-1 Accuracy	Up to ~80%
		Top-5 Accuracy	Up to ~95%

Table 2: Performance Variation with Structural Complexity

Factor Influencing Complexity	Impact on Model Performance	Specific Example
Number of Atoms in Unit Cell	Match rate decreases as the number of atoms increases [9].	XDXD match rate drops from ~70% (0-40 atoms) to ~40% (160-200 atoms) [9].
Data Resolution	Lower resolution data presents a greater challenge, though modern models are tackling this [9].	XDXD is designed for low-resolution (2.0 Ã…) single-crystal data [9].
Encoder Architecture	The choice of neural network backbone influences feature extraction efficacy [10].	For PXRDGen, a CNN-based XRD encoder outperformed a Transformer-based encoder in the structure generation module despite poorer contrastive learning performance [10].

Experimental Protocols for Benchmarking AI Models

A standardized protocol is crucial for the fair and comparable benchmarking of AI models in crystal structure determination.

Data Preparation and Preprocessing

• Source Dataset Curation: Begin with a large, diverse set of known crystal structures.
  • Primary Source: The Crystallography Open Database (COD) is a common choice due to its public accessibility and structural variety [58] [9]. For inorganic materials, the Materials Project (MP) is also widely used [10].
  • Pre-filtering: Apply filters to the raw database. For instance, exclude structures with fewer than 4 atoms or more than 256 atoms in the asymmetric unit to focus on non-trivial cases and manage computational cost [58].
• Diffraction Pattern Simulation:
  • Use a simulation package like Dans Diffraction [58].
  • Standard Parameters: Simulate patterns over a 2θ range of 5° to 90° using a Cu Kα source (wavelength λ = 1.5406 Ã…). A fixed peak width (e.g., 0.01°) is typically used, and intensities are normalized to a [0, 1] interval [58].
  • Data Augmentation: To improve model robustness, simulate patterns under different conditions (e.g., varying noise levels, peak widths) or employ signal dropout during training, such as randomly removing 0-10% of diffraction signals to mimic experimental uncertainty [9].
• Data Splitting: Randomly split the dataset into training, validation, and test sets (e.g., 80/10/10). Ensure crystal structures from the same material family are not spread across different splits to prevent data leakage.

Model Training and Evaluation

• Model Selection and Conditioning: Choose a generative model architecture, such as a diffusion model or a flow-based model [9] [10].
  • The model should be conditioned on two key inputs: the chemical formula (defining atom types and counts) and the experimental PXRD pattern (or its encoded features) [10].
  • An XRD Encoder (e.g., based on CNN or Transformer architectures) is used to convert the PXRD pattern into a latent representation that guides the structure generation process [10].
• Candidate Generation and Ranking:
  • For a given test case, generate multiple candidate structures (e.g., 16-20) by initiating the generative process from different random noise seeds [9] [10].
  • For each candidate, simulate its theoretical PXRD pattern.
  • Rank all candidates by calculating the cosine similarity between their simulated pattern and the input experimental pattern.
  • Select the top-ranked candidate as the final predicted structure [9].
• Performance Quantification:
  • Match Rate Calculation: A structure is considered "matched" if its RMSE relative to the ground truth is below a predefined threshold (e.g., a very low value). The match rate is the percentage of test samples where this condition is met. Report both 1-sample and multi-sample match rates [10].
  • Root Mean Square Error (RMSE): Calculate the RMSE of atomic coordinates for all successfully matched structures using a library like pymatgen to measure precision [9].

Table 3: Key Computational Tools for AI-Driven Crystallography

Tool Name	Type/Function	Key Use-Case in Protocol
Crystallography Open Database (COD) [58] [9]	Public Repository	Source of ground-truth crystal structures for training and testing.
Dans Diffraction [58]	Python Package	Simulation of 1D powder X-ray diffractograms from CIF files.
Pymatgen [9]	Python Library	Analysis of materials data; used for calculating RMSE between predicted and ground-truth structures.
PyTorch/TensorFlow [58]	Deep Learning Framework	Building and training neural network models (encoders, generators).
Olex2 [59]	Crystallography Software	Provides refinement engines (e.g., olex2.refine) and interfaces for quantum crystallographic refinements like HAR.
Tonto/NoSpherA2 [45] [59]	Quantum Crystallography Software	Performing Hirshfeld Atom Refinement (HAR) to generate highly accurate reference structures for benchmarking.

AI models for inorganic crystal structure determination have demonstrated remarkable performance, with leading systems achieving match rates exceeding 80% and RMSE values approaching the precision limits of traditional Rietveld refinement [10]. The benchmarking protocols outlined herein, centered on robust metrics like match rate and RMSE, provide a framework for evaluating current and future models. As these AI tools continue to evolve, they are poised to significantly automate and accelerate the materials discovery pipeline, reducing the expert time and cost required to solve and refine crystal structures from X-ray diffraction data.

Comparing X-ray Crystallography with Complementary Techniques (NMR, Cryo-EM, SAXS)

The determination of three-dimensional molecular structures is fundamental to advancing our understanding in chemistry, biology, and materials science. Structural biology has evolved significantly from its early reliance on X-ray crystallography to incorporate a suite of complementary techniques, each with distinct strengths and limitations. The primary experimental methods for atomic-level structure determination include X-ray crystallography, Nuclear Magnetic Resonance (NMR) spectroscopy, and cryo-electron microscopy (cryo-EM), while Small-Angle X-Ray Scattering (SAXS) provides valuable solution-state information for larger complexes. The scientific community has witnessed a dramatic shift in methodological preferences over the past decade. According to recent statistics, X-ray crystallography remains the dominant technique but its proportion has declined, accounting for approximately 66% of protein structures deposited in the Protein Data Bank (PDB) in 2023, while cryo-EM has experienced remarkable growth, contributing nearly 32% of new structures. NMR spectroscopy accounted for the remaining 1.9% of structures, highlighting its specialized role for smaller proteins in solution [60].

The integration of artificial intelligence with traditional structural biology methods represents the latest frontier in this field. AI-based systems like AlphaFold have revolutionized protein structure prediction from amino acid sequences, earning their developers the Nobel Prize in Chemistry in 2024 [61]. These computational advances complement rather than replace experimental methods, creating synergistic workflows that accelerate structural discovery. This article provides a comprehensive comparison of major structural biology techniques, with particular emphasis on their applications in inorganic crystal structure determination and drug development contexts.

Technical Comparison of Structural Biology Methods

Table 1: Key Characteristics of Major Structural Biology Techniques

Parameter	X-ray Crystallography	NMR Spectroscopy	Cryo-EM	SAXS
Typical Resolution	Atomic (0.8-3.0 Ã…)	Atomic (1-5 Ã… for distances)	Near-atomic to atomic (1.5-4.5 Ã…)	Low (10-100 Ã…)
Sample State	Crystalline solid	Solution	Vitrified solution	Solution
Molecular Weight Range	No upper limit, lower limit ~5 kDa	< 100 kDa (typically < 40 kDa)	> 50 kDa (optimal > 200 kDa)	10 kDa - 1 GDa
Sample Consumption	Low to moderate (single crystal)	High (hundreds of microliters at mM concentrations)	Very low (3-5 μL at low concentrations)	Moderate (tens of microliters)
Data Collection Time	Minutes to hours (synchrotron)	Days to weeks	Days	Minutes to hours
Key Limitations	Requires high-quality crystals, crystallization may be difficult	Limited to smaller proteins, signal overlap in larger systems	Smaller targets challenging, requires expertise	Low resolution, provides envelope/overall shape
Strengths	Gold standard for atomic resolution, high throughput	Studies dynamics in native-like conditions, provides atomic details without crystallization	No crystallization needed, handles large complexes and flexibility	Studies samples in solution, rapid analysis of oligomeric states

Table 2: Market Share and Growth Projections for 3D Protein Structure Analysis Technologies (2024)

Technology	Market Share (2024)	Projected Growth	Primary Applications
X-ray Crystallography	35%	Stable growth with automation	Drug discovery, small molecules, complex proteins
Cryo-Electron Microscopy	Significant growth trend	Fastest growing segment	Large complexes, membrane proteins, flexible assemblies
NMR Spectroscopy	<10%	Specialized applications	Small proteins, dynamics, drug binding
AI/Computational Tools	N/A	Exponential growth	Structure prediction, model building, data integration

The 3D protein structures analysis market size was valued at USD 2.80 billion in 2024 and is predicted to reach approximately USD 6.88 billion by 2034, expanding at a CAGR of 9.40% from 2025 to 2034 [62]. Within this market, X-ray crystallography captured the biggest technology segment share at 35% in 2024, reflecting its enduring importance in structural biology [62]. The cryo-electron microscopy segment is anticipated to show considerable growth over the forecast period, driven by its ability to analyze proteins and macromolecular complexes without crystallization [62].

The data in Table 2 reflects the evolving landscape of structural biology, where established techniques like X-ray crystallography maintain relevance through technological innovations while cryo-EM experiences rapid adoption. The integration of AI across all methodologies represents a unifying trend that enhances the capabilities of each technique [63] [62].

X-ray Crystallography: Principles and Protocols

Fundamental Principles

X-ray crystallography is based on the diffraction of X-rays by the electron clouds of atoms within a crystalline structure. When a crystal is exposed to a collimated beam of X-rays, the rays interact with the electrons in the crystal, leading to constructive and destructive interference that produces a diffraction pattern recorded on a detector [60]. The positions and intensities of the spots in the diffraction pattern are directly related to the electron density within the crystal through Bragg's Law: nλ = 2dsinθ, where λ is the wavelength of the incident X-rays, d is the distance between crystal planes, θ is the angle of incidence, and n is an integer [60].

The central challenge in X-ray crystallography remains the crystallographic phase problem - diffraction experiments measure structure factor amplitudes but lose phase information, which must be recovered through computational or experimental methods [9]. Historically, methods like direct methods, Patterson methods, and molecular replacement have been used to address this challenge, though these traditionally require high-resolution diffraction data (typically better than 1.2 Ã…) [9].

Standard Experimental Protocol

The process of X-ray crystallography involves several key steps that have been refined over decades:

• Crystallization: The target molecule must be crystallized, which often represents the most challenging step. This requires extensive screening and optimization of conditions including pH, temperature, and precipitant concentration [60]. For proteins, this step is particularly difficult as obtaining high-quality crystals suitable for diffraction can be time-consuming and unpredictable.

• Data Collection: The crystal is exposed to an X-ray beam, traditionally at synchrotron radiation sources which provide intense and highly collimated X-rays, allowing for the collection of high-resolution data [60]. Exposure times range from minutes to hours depending on crystal quality and beam intensity.

• Data Processing: The diffraction data are processed to produce a set of structure factors that describe the amplitude and phase of each diffracted beam. Phasing is critical because phase information is not directly measurable and must be inferred using methods such as molecular replacement or experimental phasing techniques like multi-wavelength anomalous dispersion (MAD) or single-wavelength anomalous dispersion (SAD) [60].

• Model Building and Refinement: An initial model of the molecule is built based on the electron density map generated from the processed data. This model is iteratively refined by adjusting atomic positions and validating the fit of the model to the experimental data, ultimately resulting in a detailed three-dimensional structure [60].

Recent innovations have addressed specific challenges in X-ray crystallography. For weakly diffracting crystals or those with limited resolution, new approaches like the application of high-voltage electric fields (2-11 kV/cm) after mounting crystals at the beamline have demonstrated on-the-fly resolution enhancement, improving diffraction quality progressively with exposure time [64]. Additionally, deep learning frameworks such as XDXD now enable end-to-end crystal structure determination directly from low-resolution single-crystal X-ray diffraction data, bypassing the need for manual map interpretation and producing chemically plausible crystal structures conditioned on the diffraction pattern [9].

Diagram 1: X-ray Crystallography Workflow. This diagram outlines the standard process from sample preparation to final structure deposition, highlighting key stages including the critical crystallization and phasing steps.

Complementary Structural Biology Techniques

Cryo-Electron Microscopy (Cryo-EM)

Cryo-EM has revolutionized structural biology by overcoming many limitations of traditional techniques. It allows scientists to visualize large macromolecular complexes and membrane proteins at near-atomic resolution without requiring crystallization [63]. The technique involves freezing samples in vitreous ice and using electron microscopy to image individual particles, which are then computationally combined to generate three-dimensional structures.

The resolution revolution in cryo-EM was triggered primarily by the development of direct electron detectors, which provide dramatically improved signal-to-noise ratios, accurate electron event counting, and rapid frame rates, enabling correction of beam-induced motion and unlocking near-atomic resolution for previously intractable targets [63]. A landmark achievement was the determination of the TRPV1 ion channel structure, which revealed how this protein detects heat and pain [63].

Cryo-EM offers particular advantages for studying complex biological systems that are difficult to crystallize, including membrane proteins, flexible assemblies, and large macromolecular complexes [63]. While initially most successful for larger complexes (>200 kDa), technical advances such as Volta phase plates have pushed the molecular weight limit down to 52 kDa for structure determination by single-particle analysis [65]. This has opened new possibilities for studying protein-free RNA structures, which have traditionally been challenging due to intrinsic heterogeneity, flexible backbones, and weak tertiary interactions [65].

Diagram 2: Cryo-EM Single Particle Analysis Workflow. This diagram illustrates the key steps in cryo-EM structure determination, from sample vitrification through particle picking, classification, and 3D reconstruction.

Nuclear Magnetic Resonance (NMR) Spectroscopy

NMR spectroscopy enables the study of macromolecules in solution, providing insights into their structural dynamics, interactions, and conformational changes [63]. Unlike X-ray crystallography, NMR does not require crystallization, making it particularly useful for analyzing small to medium-sized proteins and studying their behavior under physiological conditions [63] [60].

The technique's strengths have traditionally been in resolving the structures and dynamic properties of small to medium-sized proteins (generally <40 kDa), although advances in isotope labeling and high-field instrumentation have gradually extended these boundaries [63]. NMR has been particularly valuable for studying proteins like the oncogenic protein KRAS, which plays a crucial role in cancer signaling pathways [63].

Solid-state NMR has emerged as a powerful complement to solution NMR, particularly for membrane proteins and amyloid fibrils that are not amenable to solution studies or crystallization [63]. Despite its advantages for studying dynamics, NMR's contribution to the PDB remains relatively small (less than 10% annually), reflecting its specialized applications and technical limitations for larger systems [60].

Small-Angle X-Ray Scattering (SAXS)

SAXS is an excellent method for studying protein structure in solution, providing information about overall shape, conformational changes, and oligomeric states [61]. The technique involves scattering X-rays at small angles from samples in solution, generating data that can be used to determine low-resolution structural parameters and envelope models.

An advantage of SAXS is the ability to analyze large complexes directly in solution, allowing better control of experimental conditions and the study of dynamic behavior [61]. Scattering methods provide insights into the dynamic behavior of large macromolecular complexes and their oligomeric states in solution, complementing high-resolution techniques that may capture only static snapshots [61].

SAXS has been successfully used to study processes like the oligomerization of frataxin in solution, where the protein forms different oligomers (dimers, trimers, and higher-order oligomers) in response to higher concentrations of metals [61]. Researchers were able to follow the oligomerization process and separate different oligomeric states using SAXS, demonstrating the technique's utility for studying assembly dynamics [61].

Integrated Approaches and Recent Advancements

Hybrid Methods in Structural Biology

The integration of multiple structural biology techniques has become increasingly powerful for studying challenging biological systems. Combined approaches leverage the strengths of individual methods to overcome their respective limitations, providing more comprehensive insights into molecular structure and function.

Cryo-EM with AI-based prediction represents one of the most promising integrated approaches. The combination of cryo-EM and artificial intelligence-based structure prediction has revolutionized protein modeling by enabling near-atomic resolution visualization and highly accurate computational predictions from amino acid sequences [63]. These technologies facilitate detailed insights into challenging protein targets such as membrane proteins, flexible and intrinsically disordered proteins, and large macromolecular complexes [63].

Integrative modeling approaches combine data from multiple sources including X-ray crystallography, NMR, cryo-EM, and SAXS to reconstruct complex structures. This strategy has been used successfully to determine the structure of the nuclear pore complex, a massive molecular assembly responsible for regulating transport between the nucleus and cytoplasm [63]. Similarly, integrative approaches have been applied to study cytochrome P450 enzymes, where AlphaFold predictions have been combined with cryo-EM maps to explore conformational diversity [63].

The Ribosolve workflow exemplifies how integration of multiple techniques accelerates structure determination for challenging targets like RNA. This approach combines native gel analysis, mutate-and-map by next generation sequencing (M2-seq), cryo-EM single-particle analysis, and auto-DRRAFTER RNA modeling to enable rapid determination of previously unknown RNA structures [65]. The workflow has been successfully applied to determine structures of full-length Tetrahymena ribozyme in both apo and substrate-bound states at 3.1 Ã… resolution, revealing previously unforeseen tertiary interactions that allosterically regulate catalysis [65].

Emerging Technologies and Future Directions

Several emerging technologies are poised to further transform the landscape of structural biology:

AI-driven structure prediction tools like AlphaFold 2 and the emerging AlphaFold 3 have demonstrated remarkable accuracy in predicting protein structures from amino acid sequences alone [63]. These systems have not only accelerated the pace of structural discovery but have also made structural information more accessible to researchers worldwide, enabling a deeper understanding of molecular biology [63]. The latest release of databases includes more than 200 million predicted structures for nearly all proteins cataloged in the scientific literature, significantly enhancing our understanding of biological processes [61].

Advanced X-ray methods continue to evolve with developments like serial femtosecond crystallography (SFX) at X-ray free-electron lasers (XFELs), which has provided insights into the catalytic cycle of cytochrome c oxidase, shedding light on electron and proton transfer mechanisms [63]. Recent innovations in high-throughput screening and automated data processing further illustrate the method's ongoing relevance and adaptability [63].

Electric field enhancement in crystallography represents an innovative approach to improving data quality. Recent research has demonstrated that applying high-voltage electric fields (2-11 kV/cm) after mounting crystals at the beamline can enhance resolution on-the-fly [64]. The crystal diffraction quality improves progressively with exposure time, and up to a defined electric field threshold, the protein structure remains largely unperturbed, as confirmed by molecular dynamics simulations [64].

Table 3: Research Reagent Solutions for Structural Biology Techniques

Reagent/Equipment	Function	Technique	Key Characteristics
Direct Electron Detectors	Captures electron scattering patterns	Cryo-EM	Improved signal-to-noise, rapid frame rates, motion correction
Volta Phase Plates	Enhances image contrast	Cryo-EM	Particularly beneficial for small molecules (<100 kDa)
Crystallization Screens	Identifies optimal crystallization conditions	X-ray Crystallography	96-well or 384-well formats, varied conditions
In-situ Crystallization Plates	Allows external field application during data collection	X-ray Crystallography	Integrated electrodes for electric field application
Isotope-labeled Compounds	Enables NMR studies of biomolecules	NMR Spectroscopy	^2H, ^13C, ^15N labeling for signal assignment
Size Exclusion Chromatography	Sample purification and homogeneity assessment	Multi-technique	Critical for cryo-EM and SAXS sample quality

The field of structural biology has evolved from reliance on a single dominant technique to a multifaceted discipline that strategically employs multiple complementary methods. X-ray crystallography remains the gold standard for atomic-resolution structure determination, particularly for well-behaved proteins that form high-quality crystals. Cryo-EM has emerged as a transformative technology for studying large complexes and flexible systems that resist crystallization. NMR spectroscopy provides unique insights into protein dynamics and interactions in solution, while SAXS offers efficient characterization of overall shapes and oligomeric states in solution.

The integration of artificial intelligence with experimental methods represents the next frontier in structural biology, enabling researchers to tackle increasingly complex biological questions. Tools like AlphaFold have dramatically expanded the structural universe, while integrated workflows combine the strengths of multiple techniques to overcome individual limitations. As these technologies continue to advance, they promise to deepen our understanding of biological mechanisms and accelerate drug discovery efforts, particularly for challenging targets in human health and disease.

For researchers embarking on structural studies, the choice of technique should be guided by the biological question, sample characteristics, and available resources. In many cases, a combination of methods will provide the most comprehensive insights, leveraging the unique advantages of each approach while mitigating their individual limitations. The future of structural biology lies not in competition between techniques, but in their strategic integration to illuminate the molecular mechanisms of life.

Conclusion

The field of inorganic crystal structure determination is undergoing a transformative shift, driven by the integration of artificial intelligence with traditional crystallographic methods. AI models like PXRDGen and XDXD are breaking longstanding barriers, enabling rapid, automated, and highly accurate structure solutions from both powder and low-resolution single-crystal data. These advancements directly address critical challenges such as peak overlap and the localization of light atoms, which have historically impeded progress. For researchers and drug development professionals, robust validation remains paramount to ensure the reliability of structural models used in downstream applications. The continued evolution of these technologies promises to unlock new possibilities in materials design and biomedical research, from developing novel pharmaceuticals to engineering advanced functional materials with tailored properties. The future lies in the seamless integration of these powerful computational tools into standardized workflows, making high-quality structural insights more accessible than ever before.

References

• 1. XRD Explained: Principles, Analysis & Applications [https://www.technologynetworks.com/analysis/articles/x-ray-diffraction-xrd-xrd-principle-xrd-analysis-and-applications-404260]
• 2. X-ray Diffraction: Principles, Applications of XRD Analysis [https://gnr.it/blog/x-ray-diffraction-principles-techniques-and-applications-of-xrd-analysis/]
• 3. Understanding Bragg's Law in X-Ray Diffraction [https://www.azooptics.com/Article.aspx?ArticleID=2648]
• 4. X-ray Diffraction (XRD) Academy [https://www.thermofisher.com/us/en/home/industrial/spectroscopy-elemental-isotope-analysis/spectroscopy-elemental-isotope-analysis-learning-center/elemental-structural-analysis-information/xrd-academy.html]
• 5. X-ray crystallography [https://en.wikipedia.org/wiki/X-ray_crystallography]
• 6. x Ray crystallography - PMC - PubMed Central - NIH [https://pmc.ncbi.nlm.nih.gov/articles/PMC1186895/]
• 7. Understanding and denoting space groups - GitHub Pages [https://bruceravel.github.io/demeter/artug/atoms/space.html]
• 8. Atomsk - Tutorial - Unit cells [https://atomsk.univ-lille.fr/tutorial_unitcells.php]
• 9. XDXD: End-to-end crystal structure determination with low ... [https://arxiv.org/html/2510.17936v1]
• 10. Powder diffraction crystal structure determination using ... [https://www.nature.com/articles/s41467-025-62708-8]
• 11. Creation of crystal structure reproducing X-ray diffraction ... [https://www.nature.com/articles/s41524-023-01096-3]
• 12. Seeing Solids Clearly—Beyond Powder Patterns with ... [https://improvedpharma.com/seeing-solids-clearly-beyond-powder-patterns-single-crystal-x-ray-diffraction-polymorphs/]
• 13. Towards end-to-end structure determination from x-ray ... [https://www.nature.com/articles/s41524-024-01401-8]
• 14. Useful practices in single crystal diffraction analysis ... [https://pubs.rsc.org/en/content/articlelanding/2025/ce/d5ce00824g]
• 15. Surface structure determination by X-ray diffraction [https://www.sciencedirect.com/science/article/pii/0167572989900022]
• 16. | Geology | Proto Powder Diffraction Applications XRD [https://www.protoxrd.com/applications/geology]
• 17. - X Of Molecular ray Determination Structure [https://www.ebsco.com/research-starters/physics/x-ray-determination-molecular-structure]
• 18. Unlocking Crystal Secrets: X - Ray Crystallography [https://www.numberanalytics.com/blog/ultimate-guide-to-x-ray-crystallography-in-inorganic-chemistry]
• 19. Application of X - ray Diffraction and Electron Crystallography for... [https://pubmed.ncbi.nlm.nih.gov/29091406/]
• 20. Rietveld Refinement - an overview [https://www.sciencedirect.com/topics/materials-science/rietveld-refinement]
• 21. Accuracy in Rietveld quantitative phase analysis [https://pmc.ncbi.nlm.nih.gov/articles/PMC4886975/]
• 22. Phase problem [https://en.wikipedia.org/wiki/Phase_problem]
• 23. A general strategy to solve the phase problem in RNA ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC1995091/]
• 24. A general method for directly phasing diffraction data from ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC9438493/]
• 25. A deep-learning technique for phase identification in ... [https://www.nature.com/articles/s41467-019-13749-3]
• 26. XDXD: End-to-end crystal structure determination with low ... [https://arxiv.org/abs/2510.17936]
• 27. Powder Diffraction Crystal Structure Determination Using ... [https://arxiv.org/abs/2409.04727]
• 28. Crystal Structure of the Novel Ternary Indide ErCo2In [https://link.springer.com/article/10.1007/s40192-025-00400-x]
• 29. Crystal Structure Determination of XRD Data [https://www.malvernpanalytical.com/en/products/measurement-type/crystal-structure-determination]
• 30. Laboratory-based X-ray diffractometer with fast time ... [https://www.sciopen.com/article/10.26599/EMD.2025.9370057]
• 31. Exploring the transferability of machine-learning models for ... [https://pubs.rsc.org/en/content/articlehtml/2025/dd/d4dd00400k]
• 32. Enhancing phase characterization of AlCuCrFeNi high ... [https://www.sciencedirect.com/science/article/pii/S223878542500657X]
• 33. Basics to powder X-ray diffraction: How to achieve high- ... [https://www.malvernpanalytical.com/en/learn/knowledge-center/insights/basics-to-powder-x-ray-diffraction-how-to-achieve-high-quality-xrd-patterns-qa]
• 34. Part 1: Observing Hydrogen | Element Strategy Initiative [https://www.mext.go.jp/elements-strategy/en/limit/series1]
• 35. Powder diffraction crystal structure determination using ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC12340088/]
• 36. XRD Basics [https://www.physics.upenn.edu/~heiney/datasqueeze/basics.html]
• 37. Neutron imaging of lithium batteries [https://www.sciencedirect.com/science/article/pii/S2542435121005766]
• 38. 4D imaging of lithium-batteries using correlative neutron ... [https://www.nature.com/articles/s41467-019-13943-3]
• 39. A Comprehensive Review of Spectroscopic Techniques for ... [https://www.spectroscopyonline.com/view/a-comprehensive-review-of-spectroscopic-techniques-for-lithium-ion-battery-analysis]
• 40. X-Ray Crystallography Goes Even Tinier [https://vcresearch.berkeley.edu/news/x-ray-crystallography-goes-even-tinier]
• 41. Sample delivery methods for protein X-ray crystallography ... [https://www.nature.com/articles/s41467-025-65173-5]
• 42. Standard Sample Preparation for Serial Femtosecond ... [https://www.mdpi.com/2218-273X/15/11/1488]
• 43. (IUCr) A good-practice guide to solving and refining molecular ... [https://journals.iucr.org/c/issues/2025/10/00/ky3231/]
• 44. Powder X-ray diffraction assisted evolutionary algorithm for ... [https://pubs.rsc.org/en/content/articlehtml/2025/dd/d4dd00269e]
• 45. A quantum crystallographic protocol for general use [https://www.nature.com/articles/s41598-025-96400-0]
• 46. Stereochemistry and Validation of Macromolecular Structures [https://pmc.ncbi.nlm.nih.gov/articles/PMC5560084/]
• 47. X-ray crystallography: Assessment and validation of protein ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC3138648/]
• 48. Validation and Quality Assessment of X-ray Protein Structures [https://www.proteinstructures.com/protein-structure-validation/]
• 49. A New Generation of Crystallographic Validation Tools for ... [https://www.sciencedirect.com/science/article/pii/S0969212611002851]
• 50. R-factor (crystallography) [https://en.wikipedia.org/wiki/R-factor_(crystallography)]
• 51. Reliability factor, R-factor | Glossary [https://www.jeol.com/words/emterms/20190605.092806.php]
• 52. Root mean square deviation [https://en.wikipedia.org/wiki/Root_mean_square_deviation]
• 53. Ramachandran Plot - Proteopedia, life in 3D [https://proteopedia.org/wiki/index.php/Ramachandran_plots]
• 54. MolProbity: More and better reference data for improved all ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC5734394/]
• 55. Structure Validation and Quality [https://www.rcsb.org/docs/additional-resources/structure-validation-and-quality]
• 56. Validation of Structures in the Protein Data Bank - PMC [https://pmc.ncbi.nlm.nih.gov/articles/PMC5718880/]
• 57. Multivariate Analyses of Quality Metrics for Crystal Structures ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC7182075/]
• 58. A new benchmark for machine learning applied to powder ... [https://www.nature.com/articles/s41597-025-05534-3]
• 59. Benchmarking crystal structure refinement: A systematic ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC12422757/]
• 60. Comparison of X-ray Crystallography, NMR and EM [https://www.creative-biostructure.com/comparison-of-crystallography-nmr-and-em_6.htm?srsltid=AfmBOopKHqP5oLZABh0EKMJgq80LzlsTWmddUGzYQou-P9MOsJ3oRqgm]
• 61. Introduction to the Experimental Methods in Structural Biology [https://www.proteinstructures.com/experimental-methods-structural-biology/]
• 62. 3D Protein Structures Analysis Market Size 2025 to 2034 [https://www.precedenceresearch.com/3d-protein-structures-analysis-market]
• 63. High-resolution protein modeling through Cryo-EM and AI [https://pmc.ncbi.nlm.nih.gov/articles/PMC12590954/]
• 64. On-the-fly resolution enhancement in X-ray protein ... [https://link.springer.com/article/10.1007/s00249-025-01731-5]
• 65. Cryo-EM advances in RNA structure determination [https://www.nature.com/articles/s41392-022-00916-0]