Automated SCF Convergence for Robust Geometry Optimization in Computational Drug Discovery

Abstract

This article provides a comprehensive guide for researchers and drug development professionals on automating Self-Consistent Field (SCF) convergence to achieve reliable and efficient molecular geometry optimization. It covers foundational SCF principles and common convergence challenges, explores advanced algorithms and their implementation in major quantum chemistry packages, details systematic troubleshooting protocols for difficult systems, and establishes validation frameworks for benchmarking performance. By integrating these strategies, scientists can enhance the accuracy and throughput of computational workflows critical for biomolecular modeling, ligand-receptor interaction studies, and materials design.

Understanding SCF Convergence: The Engine of Quantum Chemical Geometry Optimization

The Critical Role of SCF Convergence in Determining Molecular Structure and Energetics

Self-Consistent Field (SCF) convergence is a foundational step in quantum chemical calculations, directly determining the accuracy and reliability of computed molecular structures and energies. Failure to achieve convergence halts workflows and jeopardizes research outcomes. This guide provides targeted troubleshooting strategies, framed within automated SCF convergence research, to help scientists efficiently resolve these critical computational challenges.

Understanding SCF Convergence: Core Concepts and FAQs

What is SCF Convergence and Why is it Critical?

The SCF procedure iteratively solves for the electronic structure of a molecule until the energy and electron density stop changing significantly. Successful convergence is the prerequisite for any subsequent calculation of molecular properties, reaction pathways, or spectroscopic predictions. Within automated workflows, robust convergence is essential for high-throughput screening and machine learning potential generation, where thousands of calculations must run without manual intervention [1].

What Are the Physical Reasons for SCF Non-Convergence?

Several physical scenarios in a molecular system can prevent the SCF procedure from converging [2]:

• Small HOMO-LUMO Gap: When the highest occupied and lowest unoccupied molecular orbitals are close in energy, even small changes in the electron density can cause electrons to "slosh" back and forth between them, leading to oscillatory behavior [2].
• Charge Sloshing: In systems with high polarizability (often related to a small HOMO-LUMO gap), a small error in the Kohn-Sham potential can cause a large distortion in the electron density. This can create a feedback loop where the potential becomes increasingly erroneous, leading to divergence [2].
• Incorrect Initial Electron Density Guess: A poor starting point for the electron density can lead the optimization down a path to divergence, especially for systems with unusual charge/spin states or metal centers [2].
• Incorrect Symmetry: Imposing artificially high symmetry on a molecule can sometimes force a degenerate electronic state with a zero HOMO-LUMO gap, making convergence impossible [2].

Troubleshooting Guide: A Structured Approach

Adopt a step-by-step methodology to diagnose and resolve SCF convergence issues. The following workflow provides a logical escalation path.

Step 1: Fundamental Checks

Before adjusting complex parameters, verify the basics.

• Inspect Molecular Geometry: Ensure interatomic distances and angles are chemically sensible. Geometries with nearly dissociated atoms or severely strained bonds are challenging to converge [3].
• Verify Charge and Multiplicity: An incorrect spin state can prevent convergence, especially for transition metal complexes [2].

Step 2: Improve the Initial Electron Density Guess

A high-quality initial guess can dramatically improve SCF stability.

• Use Advanced Guess Methods: Switch from the default core Hamiltonian to extended Hückel (guess=huckel), SAD (Superposition of Atomic Densities), or fragment-based guesses if available in your software [4].
• Reuse Converged Wavefunctions: Perform a quick calculation with a simpler method or basis set, then use the resulting wavefunction as the initial guess (guess=read) for the target calculation [4].
• Leverage Machine Learning: Emerging ML models can predict accurate initial electron densities, significantly reducing SCF cycles [5].

Step 3: Adjust SCF Algorithm Parameters

Tweak the SCF solver's behavior to stabilize convergence.

• Apply Level Shifting: Artificially increase the energy of virtual orbitals to reduce mixing with occupied orbitals. For example, in Gaussian, use SCF=vshift=300 (values of 300-500 are common). This affects only the convergence process, not the final results [4].
• Modify Electron Density Mixing: Reduce the mixing parameter (AMIX and BMIX in VASP; Mixing in BAND) for a more conservative, stable update of the density between cycles [6].
• Change the Algorithm: Switch between DIIS, QC (Quadratic Converger), or the MultiSecant method. If DIIS causes oscillations, try SCF=NoDIIS or SCF=QC [4] [6].

Step 4: Increase Numerical Accuracy

Inaccurate numerical evaluation of integrals can cause noise that prevents convergence.

• Use a Finer Integration Grid: For DFT calculations, specify a finer numerical integration grid (e.g., int=ultrafine in Gaussian). This is particularly important for meta-GGA and hybrid functionals, and for systems with diffuse functions [4].
• Tighten SCF Convergence Criterion: Counter-intuitively, using a tighter convergence criterion (e.g., SCF%Convergence 1e-7 or 1e-8) can sometimes help avoid oscillations near the solution by providing a more consistent gradient [7].
• Improve Basis Set Quality: Increase the basis set numerical quality (e.g., to Good or VeryGood), which often improves the accuracy of computed forces and the stability of the SCF procedure [7].

Step 5: Advanced System-Specific Strategies

• Use Fermi Broadening: Applying a finite electronic temperature (SCF=Fermi) can occasionally help by smearing orbital occupations [4]. Be aware this moves the calculation away from the pure ground state.
• Two-Step Optimization for Challenging Systems: For difficult systems like magnetic metals or those requiring meta-GGA functionals, a multi-step approach is effective [8]:
  • Converge with a simpler functional (e.g., PBE).
  • Restart using the resulting wavefunction with a more advanced functional (e.g., MBJ) and a conservative solver setting (ALGO=All in VASP, TIME=0.1).

Specialized Protocols for Challenging Systems

Protocol for Systems with a Small HOMO-LUMO Gap

Systems with small gaps (e.g., transition metal complexes, open-shell species, or distorted geometries) are prone to charge sloshing and orbital flipping [2].

Detailed Methodology:

• Diagnose: Check the HOMO-LUMO gap after the first SCF cycle. If it is less than ~0.5 eV, the system is in the high-risk category.
• Apply Level Shifting: This is the most direct remedy. Use SCF=vshift=500 in Gaussian or an equivalent keyword to increase the HOMO-LUMO gap artificially during the convergence process [4].
• Use Fermi Smearing or Fractional Occupations: Set ISMEAR = -1 (VASP) or SCF=Fermi (Gaussian) to assign fractional occupations to orbitals near the Fermi level, which can dampen oscillations [8].
• Lock Occupations: If oscillations are due to electrons flipping between specific orbitals, use the OCCUPATIONS block (ADF) or the Maximum Overlap Method (MOM) to freeze the occupation pattern [7] [5].

Protocol for Excited State and Solvation Calculations

Calculations involving excited states (e.g., ΔSCF) or implicit solvation models are inherently less stable [3] [5].

Detailed Methodology:

• Converge in Gas Phase First: Perform a single-point energy calculation in the gas phase for the target electronic state. For excited states, this may require specialized algorithms like MOM or cDFT [5].
• Use the Gas-Phase Wavefunction as a Guess: Read the converged gas-phase wavefunction as the initial guess for the solvated or excited-state calculation (guess=read) [4].
• Tighten SCF and Grid Settings: When using a Polarizable Continuum Model (PCM), combine it with a finer integration grid (int=ultrafine) to minimize numerical noise that can disrupt convergence [4].

Protocol for Magnetic Systems (LDA+U)

Magnetic systems, particularly with LDA+U, are prone to convergence issues due to delicate energy balances between spin configurations [8].

Detailed Methodology:

• Step 1 - Preliminary Spin-Polarized Calculation: Run a spin-polarized calculation without LDA+U (ICHARG=12, ALGO=Normal) to get a reasonable initial spin density.
• Step 2 - Stable Solver with Reduced Time Step: Restart from Step 1's output, switching to a more stable solver (ALGO=All in VASP) and reducing the effective time step (TIME=0.05).
• Step 3 - Introduce LDA+U: Restart again from Step 2's output, now adding the LDA+U parameters while keeping the stable solver and small time step [8].

The Scientist's Toolkit: Essential Reagents and Solutions

The table below catalogs key "research reagents" – computational parameters and tools – used to troubleshoot SCF convergence.

Research Reagent	Function & Purpose	Example Usage / Notes
Level Shift	Increases virtual orbital energies, widening the HOMO-LUMO gap to prevent oscillation.	SCF=vshift=400 (Gaussian). A primary tool for small-gap systems [4].
Fermi Smearing	Smears electron occupation, stabilizing metallic and small-gap systems.	ISMEAR = -1 (VASP), SCF=Fermi (Gaussian). Introduces small entropy term [8].
DIIS/QC Algorithm	DIIS accelerates convergence; QC is slower but more robust for difficult cases.	Switch to SCF=QC if SCF=DIIS fails [4].
Fine Integration Grid	Increases accuracy of numerical integrals, reducing noise.	int=ultrafine (Gaussian). Critical for DFT with diffuse functions [4].
Density Mixing Parameters	Controls how the new Fock matrix is mixed with the old. Reducing mixing stabilizes convergence.	AMIX = 0.02 (VASP), SCF{Mixing 0.05} (BAND) for conservative updates [6].
Advanced Initial Guess	Provides a better starting electron density, reducing SCF cycles.	guess=huckel, or guess=read from a simpler calculation [4].
Solvation Model	Mimics solvent effects but can introduce convergence instability.	Converge in gas phase first, then use guess=read for PCM calculation [4].
GTP-gamma-S 4Li	GTP-gamma-S 4Li, MF:C10H12Li4N5O13P3S, MW:563.1 g/mol	Chemical Reagent
N-Acetyl-N-methyl-L-leucine	N-Acetyl-N-methyl-L-leucine|C9H17NO3|187.24 g/mol

Advanced Diagnostics and Automation

Interpreting SCF Output for Diagnostics

Automated scripts can parse SCF output logs to classify the failure mode and suggest remedies.

• Oscillatory Behavior: If the energy difference between cycles alternates in sign with a large amplitude (>1x10⁻³ Hartree), it suggests a small HOMO-LUMO gap or charge sloshing. Prescription: Apply level shifting or reduce density mixing [2] [4].
• Steady Drift: If the energy decreases/increases steadily over many cycles, the initial geometry may be far from equilibrium or the initial guess is very poor. Prescription: Check geometry, improve the initial guess, or simply allow more cycles [7].
• Trailing Convergence: The energy change is consistently small but just above the convergence threshold. This is often due to numerical noise. Prescription: Tighten the integration grid or SCF convergence criteria [5] [2].

Towards Full Automation: Adaptive SCF Protocols

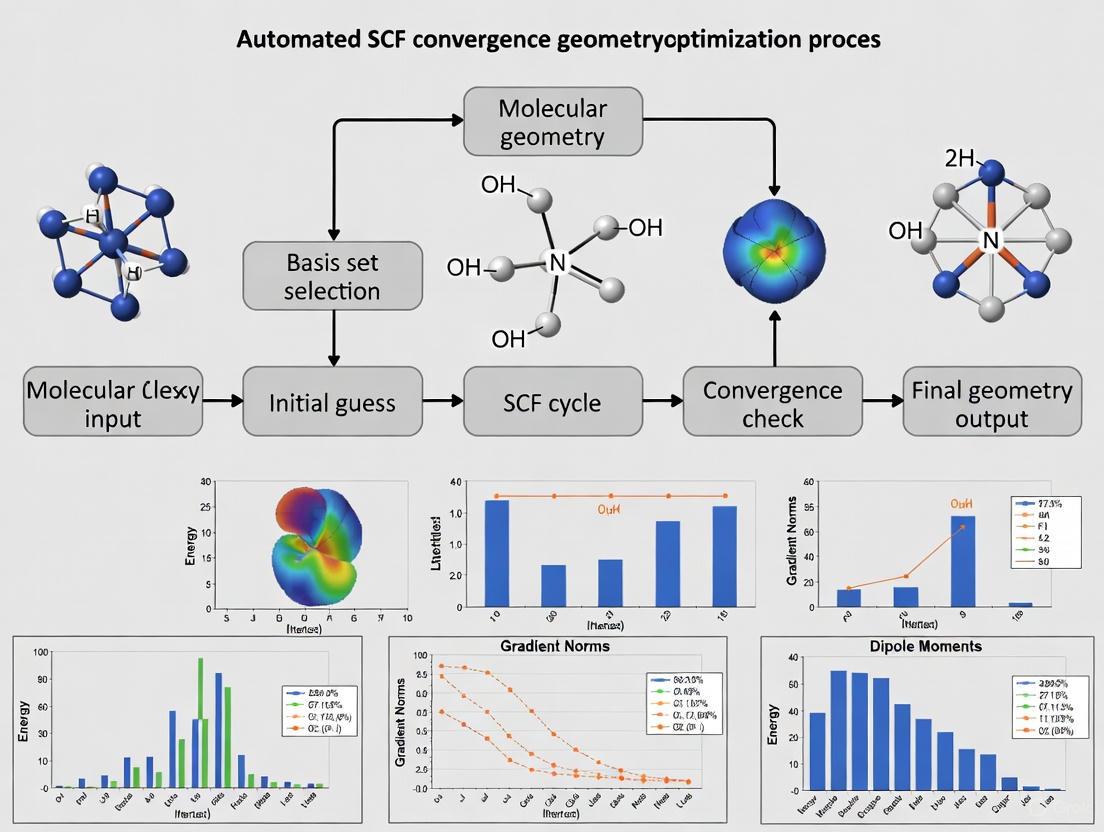
For fully automated workflows (e.g., in high-throughput virtual screening), adaptive protocols that modify parameters on-the-fly are essential. The logic for such a system can be visualized as follows:

This automated troubleshooting guide provides a systematic framework for researchers to diagnose and resolve SCF convergence issues, enhancing the reliability of automated computational workflows in drug development and materials science.

Troubleshooting Guides

How can I resolve SCF energy oscillations?

SCF energy oscillations, where the total energy jumps between two or more values instead of converging, indicate that the iterative process is trapped in a limit cycle [9]. This is a non-linear phenomenon common in systems with complex electronic structures, such as open-shell transition metal compounds or metallic systems [10] [6].

Diagnosis and Resolution Protocol:

• Diagnose the Pattern: First, examine the last ten or more SCF iterations. Oscillations are confirmed if the energy jumps back and forth between distinct values around a specific point, while the energy gradient shows little change [7].
• Apply Damping: Use more conservative settings to dampen the oscillations. This can be achieved by decreasing the SCF mixing parameter or using dedicated keywords like SlowConv or VerySlowConv [10] [6].
• Change the SCF Algorithm: If the default DIIS method is oscillating, switch to a more robust algorithm. Geometric Direct Minimization (GDM) is highly recommended as a fallback, as it properly accounts for the geometry of the orbital rotation space [11]. Alternatively, second-order convergence methods like the Trust Radius Augmented Hessian (TRAH) can be employed [10].
• Adjust DIIS Parameters: For pathological cases, increasing the number of Fock matrices stored in the DIIS subspace (DIISMaxEq) can improve extrapolation. For very difficult systems, values between 15 and 40 (default is 5) may be necessary [10].
• Improve Numerical Accuracy: Increase the grid quality for numerical integration and tighten the SCF convergence criterion to reduce numerical noise that can hinder convergence [7] [10].

Table: Resolution Strategies for SCF Oscillations

Strategy	Specific Action	Expected Outcome
Algorithm Change	Switch from DIIS to GDM or TRAH [11] [10].	More stable, monotonic convergence.
Damping	Use ! SlowConv or reduce SCF%Mixing to 0.05 [10] [6].	Reduced energy jumps between cycles.
DIIS Enhancement	Increase DIISMaxEq to 15-40 and/or set directresetfreq to 1 [10].	Improved extrapolation and removal of numerical noise.
Guess Improvement	Use MORead to import orbitals from a converged, simpler calculation (e.g., BP86/def2-SVP) [10].	A starting point closer to the solution, reducing initial instability.

The following workflow provides a systematic method for diagnosing and resolving SCF oscillations:

How do I stabilize SCF convergence for systems with small HOMO-LUMO gaps?

Systems with small or vanishing HOMO-LUMO gaps, such as metals or diradicals, are prone to SCF convergence issues because tiny changes in geometry can cause significant changes in the electronic structure (orbital repopulation) [7].

Diagnosis and Resolution Protocol:

• Verify the Ground State: Perform a single-point calculation and check that you have the correct electronic ground state. Confirm that the spin polarization value is correct. For open-shell systems, try calculating high-spin states to see if they are lower in energy [7].
• Increase SCF Accuracy: Tighten the SCF convergence criterion (e.g., to 1e-8) and increase the numerical quality (e.g., to "Good") to ensure forces and energies are calculated with high precision [7].
• Lock Orbital Occupations: If electronic structure changes between steps are the problem, manually freeze the number of electrons per irreducible representation using an OCCUPATIONS block. This prevents orbital repopulation that disrupts convergence [7].
• Use Finite Electronic Temperature: In geometry optimizations, applying a small finite electronic temperature (e.g., Convergence%ElectronicTemperature) can smear orbital occupations, making the initial SCF cycles easier. This temperature can be automated to decrease as the optimization proceeds and the geometry nears convergence [6].
• Employ Robust Algorithms: Use second-order convergence algorithms like TRAH or GDM, which are designed to handle difficult convergence landscapes [10] [11].

Table: Strategies for Small HOMO-LUMO Gap Systems

Strategy	Specific Action	Rationale
Increase Precision	Set NumericalQuality Good and SCF converge 1e-8 [7].	Ensures accurate gradients despite near-degeneracy.
Control Occupations	Use an OCCUPATIONS block to freeze electrons per symmetry [7].	Prevents erratic orbital flipping during optimization.
Smear Occupations	Use Convergence%ElectronicTemperature (e.g., 0.01 Hartree) [6].	Stabilizes initial SCF cycles by damping occupation changes.
Advanced Algorithms	Enable AutoTRAH or use SCF_ALGORITHM GDM [10] [11].	Provides stronger convergence for near-degenerate systems.

What are the best practices for modeling charge-transfer systems?

Charge-transfer (CT) systems, characterized by donor-bridge-acceptor (D-σ-A) architectures, require careful treatment to accurately model their electronic and optical properties, which are highly sensitive to geometry and external fields [12].

Modeling and Optimization Protocol:

• Thorough Initial Optimization: Optimize molecular structures to a minimum on the potential energy surface for multiple spin states (closed-shell singlet, open-shell singlet, triplet). This ensures the correct electronic state is identified [12].
• Investigate Electric Field Response: CT systems are used in devices under electric fields. Re-optimize geometries under an applied electric field (e.g., from -0.30 V/Ã… to 0.50 V/Ã…) to study the response of the HOMO-LUMO gap, orbital energies, and total dipole moment [12].
• Analyze Frontier Orbitals: Calculate the HOMO-LUMO gap and inspect the spatial distribution of these orbitals. In a proper CT system, HOMO should be localized on the donor and LUMO on the acceptor moiety [12].
• Ensure Method Consistency: Use the same functional and basis set across all calculations for a given system to ensure result comparability. For example, employ the B3LYP functional with the 6-31G(d) basis set for geometry optimization and subsequent property calculations [12].

Table: Key Properties to Calculate for Charge-Transfer Systems

Property	Calculation Method	Significance in CT Systems
HOMO-LUMO Gap	DFT single-point energy calculation on optimized geometry [12].	Indicates intrinsic conductivity; a small gap facilitates charge transfer.
Orbital Localization	Visualize HOMO and LUMO isosurfaces [12].	Confirms charge-transfer character (HOMO on donor, LUMO on acceptor).
Dipole Moment	Calculate from electron density [12].	Measures molecular polarity; can be strongly affected by an external field.
Field-Dependent Gap	Re-optimize geometry under a range of electric fields [12].	Models device operation; gap narrowing under field indicates improved conduction.

The following workflow outlines the key steps for modeling charge-transfer systems, from setup to analysis:

Frequently Asked Questions (FAQs)

Q1: My geometry optimization does not converge, but the SCF seems fine. What should I check? A1: If the SCF is converging but the geometry optimization is stuck, the problem likely lies in the accuracy of the calculated energy gradients (forces). To improve gradient accuracy, you can:

• Increase the numerical quality (e.g., NumericalQuality Good).
• Use an exact density keyword or select "Exact" for the density in the XC-potential.
• Tighten the SCF convergence criteria [7]. Additionally, check if constraints are breaking the molecular symmetry and consider switching to delocalized internal coordinates, which often converge faster than Cartesian coordinates [7].

Q2: Why are my optimized bond lengths significantly too short? A2: Excessively short bond lengths, particularly for heavy elements, often indicate a basis set problem. Two common causes are:

• Onset of Pauli variational collapse: This can occur when using the Pauli relativistic method with small frozen cores and large basis sets.
• Overlapping frozen cores: As atoms approach, overlapping frozen cores cause missing repulsive terms, leading to spurious "core collapse." The best solution is to abandon the Pauli method and use the ZORA relativistic approach instead. If you must use Pauli, apply larger frozen cores or reduce the flexibility of the basis set's s- and p-functions [7].

Q3: What should I do if my SCF calculation converges to the wrong state? A3: This can happen with a poor initial guess. To guide the calculation to the desired state:

• Use the Maximum Overlap Method (MOM), which enforces occupation of a continuous set of orbitals to prevent flipping between different states [11].
• Manually construct a guess by converging a closed-shell, oxidized, or reduced state of the system, and then use those orbitals (MORead) as the starting point for the target calculation [10].

The Scientist's Toolkit: Research Reagent Solutions

Table: Essential Computational Tools for SCF and Geometry Optimization Research

Tool / 'Reagent'	Function	Example Use Case
GDM Algorithm	A robust geometric direct minimization SCF algorithm [11].	Primary algorithm for restricted open-shell systems or fallback when DIIS fails.
TRAH-SCF	A robust second-order SCF converger (Trust Radius Augmented Hessian) [10].	Automated fallback for difficult systems (e.g., open-shell transition metals).
DIISMaxEq	Input parameter controlling the number of Fock matrices in DIIS extrapolation [10].	Set to 15-40 for pathological cases to improve convergence stability.
Finite Electronic Temperature	Smears orbital occupations via an electronic temperature (kT in Hartree) [6].	Stabilizing initial SCF cycles in geometry optimizations of metallic systems.
OCCUPATIONS Block	Input block to manually fix orbital occupations [7].	Preventing unwanted orbital repopulation in systems with small HOMO-LUMO gaps.
B3LYP/6-31G(d)	A standard DFT functional and basis set combination [12].	Benchmark studies and geometry optimization of organic charge-transfer systems.
Fmoc-N-Me-D-Glu-OH	Fmoc-N-Me-D-Glu-OH, MF:C21H21NO6, MW:383.4 g/mol	Chemical Reagent
5-azido-2H-1,3-benzodioxole	5-azido-2H-1,3-benzodioxole, MF:C7H5N3O2, MW:163.13 g/mol	Chemical Reagent

Frequently Asked Questions

Q1: What is the primary advantage of using a Superposition of Atomic Densities (SAD) guess over a Core Hamiltonian guess? The SAD guess is typically much better than starting from a core Hamiltonian. It is often easier to implement and provides a superior starting point for the SCF procedure, leading to faster and more reliable convergence, especially for open-shell systems. [13]

Q2: My SCF calculation fails to converge, even with a SAD guess. What are the next steps? When facing persistent convergence issues, you can:

• Use more conservative SCF settings, such as decreasing the mixing parameter or reducing the DIIS subspace size. [6]
• Try an alternative algorithm like the MultiSecant method, which has a similar cost per iteration to DIIS, or the LISTi method. [6]
• Improve numerical accuracy by increasing the integration grid quality or improving the density-fitting precision, as poor numerical quality can cause convergence failure. [6]

Q3: Can a good initial guess reduce computational time in geometry optimizations? Yes, significantly. A high-quality initial guess can lead to faster SCF convergence in each geometry step. Furthermore, within a geometry optimization, you can use automations to start with a looser SCF convergence criterion and a higher electronic temperature when the nuclear gradients are large, tightening these parameters as the geometry approaches its minimum. [6]

Q4: How can machine learning models contribute to initial guess generation? Machine learning models, such as the SchNOrb framework, can be trained to predict the Hamiltonian matrix in an atomic orbital basis. This predicted Hamiltonian can then be used to generate molecular orbitals, providing an excellent starting point for the SCF procedure and drastically reducing the number of SCF iterations required. [14]

Q5: Are there open-source libraries available to help with SCF convergence? Yes. Libraries like OpenOrbitalOptimizer provide reusable, state-of-the-art SCF solvers, implementing various convergence accelerators like DIIS, EDIIS, ADIIS, and the Optimal Damping Algorithm (ODA). These can be integrated into existing quantum chemistry codes to improve robustness. [15]

Troubleshooting Guides

Problem: SCF Calculation Fails to Converge

Issue: The self-consistent field procedure oscillates or diverges, failing to find a solution.

Diagnosis and Resolution:

• Step 1: Check the Initial Guess
  • Symptom: Large initial energy error or erratic behavior from the first iteration.
  • Action: Switch from the core Hamiltonian guess to a Superposition of Atomic Densities (SAD). [13] For systems with heavy elements, ensure the frozen core approximation is not hindering convergence; using a small or no frozen core may help. [6]

• Step 2: Adjust SCF Algorithm Parameters

  • Symptom: Convergence stalls after initial improvement or oscillates.
  • Action: Tighten the SCF convergence parameters. Implement more robust algorithms via input settings, for example:
    Alternatively, switch to a different algorithm like SCF%Method MultiSecant. [6]

• Step 3: Improve Numerical Precision

  • Symptom: Many iterations occur after the calculation is "halfway" converged.
  • Action: Increase the NumericalQuality setting. For systems with heavy elements, ensure the Becke integration grid quality is sufficient. Using only one k-point can also be a source of problems in periodic systems. [6]

• Step 4: For Geometry Optimizations - Use Adaptive Settings

  • Symptom: SCF convergence is problematic during the early stages of a geometry optimization when the nuclear gradients are still large.
  • Action: Use engine automations to dynamically adjust SCF parameters based on the optimization progress. This allows for a higher electronic temperature and looser SCF convergence at the start, refining them as the geometry converges. [6] Example automation block:

Problem: Geometry Optimization Does Not Converge

Issue: The geometry optimization exceeds the maximum number of steps without meeting the convergence criteria.

Diagnosis and Resolution:

• Prerequisite: Ensure the SCF convergence is robust at each geometry step. Unstable SCF can cause noisy gradients that prevent geometry convergence. [6]
• Improve Gradient Accuracy: If SCF is stable but geometry is not, the gradients may be numerically inaccurate. Increase the basis set integration quality (e.g., RadialDefaults%NR 10000) and set NumericalQuality Good. [6]
• Check for Saddle Points: The optimization may have converged to a transition state instead of a minimum. Enable Properties%PESPointCharacter True and set GeometryOptimization%MaxRestarts to a value >0 (e.g., 5) with UseSymmetry False. This allows the optimizer to automatically detect saddle points and restart with a displacement along the imaginary mode to find the minimum. [16]

Comparison of Initial Guess Methodologies

The table below summarizes the key characteristics of different initial guess methods.

Method	Core Principle	Typical Use Case	Advantages	Limitations
Core Hamiltonian	Neglects electron-electron interactions, using only the one-electron part of the Hamiltonian.	Simple systems, default fallback.	Simple to compute.	Often a poor guess, can lead to slow SCF convergence or failure. [13]
Superposition of Atomic Densities (SAD)	Sums pre-computed atomic electron densities to form the initial molecular density.	General purpose for both closed-shell and open-shell systems.	More physically realistic than core Hamiltonian, easier and often better than a minimal basis calculation. [13]	Effectiveness can depend on the atomic configurations and potentials used. [17]
Machine Learning (e.g., SchNOrb)	A deep neural network predicts the Hamiltonian matrix in an atomic orbital basis from the molecular structure.	Suitable for organic molecules; promising for inverse design and property-focused optimization.	Provides a near-quantitative guess, can speed up SCF by orders of magnitude; gives access to electronic properties. [14]	Requires training data and model; performance may vary for molecules far from training set.

Experimental Protocols

Protocol 1: Implementing a SAD Guess with Fitted Potentials

This methodology outlines an efficient approach to implement the SAD guess in Gaussian-basis codes using error function fits to fully numerical atomic radial potentials. [17]

• Atomic Potential Calculation: For each element, perform fully numerical density functional calculations (e.g., at the exchange-only LDA level on top of Hartree-Fock densities) to obtain spherically symmetric atomic potentials.
• Potential Fitting: Fit the fully numerical radial potentials using a linear combination of error functions. This allows the potential to be expressed in a form compatible with Gaussian-basis integral evaluation.
• Integration: Precompute and report the fitting coefficients for the entire periodic table. These coefficients can be used in any quantum chemistry code to construct the initial guess Fock matrix in terms of standard two-electron integrals.
• Application: For a new molecule, the initial guess is formed by summing the fitted atomic potentials for all atoms in the system.

Protocol 2: Using a Machine-Learned Hamiltonian as an Initial Guess

This protocol uses the SchNOrb deep learning framework to generate a high-quality initial guess for the SCF calculation. [14]

• Model Training:
  • Data Generation: Create a dataset of organic molecules with pre-computed quantum chemical properties (Hamiltonian and overlap matrices) at a chosen level of theory.
  • Architecture: Employ the SchNOrb architecture, which extends an atomistic neural network (SchNet) to represent the electronic Hamiltonian.
  • Feature Construction: Build symmetry-adapted pairwise features for atom pairs to represent the Hamiltonian matrix blocks, ensuring rotational invariance and covariance.
• Prediction:
  • Input: The 3D molecular structure is fed into the trained SchNOrb model.
  • Output: The model predicts the full Hamiltonian matrix (H) in the local atomic orbital basis.
• SCF Restart:
  • The predicted Hamiltonian matrix is used to solve the generalized eigenvalue equation (Hc = εSc) to obtain an initial set of molecular orbitals and eigenvalues.
  • This ML-predicted wavefunction is then used as the starting point for the conventional SCF procedure, significantly reducing the number of iterations required to reach convergence.

Workflow Visualization

The following diagram illustrates the logical workflow for selecting and applying an initial guess methodology within an automated SCF convergence framework.

The Scientist's Toolkit: Research Reagent Solutions

This table details key software and algorithmic "reagents" essential for experiments in automated SCF convergence.

Item	Function	Application Context
LibXC	A library of exchange-correlation functionals.	Provides standardized, portable implementations of density functionals for DFT calculations, "unbundling" DFT development. [5]
OpenOrbitalOptimizer	A reusable open-source C++ library for SCF solvers.	Implements standard algorithms (DIIS, EDIIS, ADIIS, ODA) to accelerate SCF convergence; can be integrated into legacy codes. [15]
SchNOrb	A deep neural network for predicting molecular wavefunctions.	Generates a quantum-mechanically informed initial guess for the Hamiltonian, drastically reducing SCF iterations and enabling inverse design. [14]
Superposition of Atomic Potentials (SAP)	An efficient method for generating initial guesses via fitted atomic potentials.	Provides a robust and systematically improvable starting density for SCF calculations in Gaussian-basis codes. [17]
Engine Automations (AMS)	Dynamically adjusts SCF parameters during a geometry optimization.	Maintains SCF stability by using looser criteria at the start of an optimization and tighter criteria near convergence. [6]
N3-methylbutane-1,3-diamine	N3-Methylbutane-1,3-diamine	N3-Methylbutane-1,3-diamine (CAS 41434-26-8) is a chemical compound for research use only. It is not for human or animal consumption.
N-Acetyl-3-hydroxy-L-valine	N-Acetyl-3-hydroxy-L-valine

The Direct Inversion in the Iterative Subspace (DIIS) algorithm, developed by Peter Pulay, is one of the most successful and widely used convergence acceleration techniques in electronic structure calculations [18] [11] [19]. Within the context of automated Self-Consistent Field (SCF) convergence for geometry optimization research, DIIS addresses a fundamental challenge: the slow convergence or outright failure of traditional SCF iterative methods, particularly for chemically complex systems like transition metal complexes or molecules with small HOMO-LUMO gaps [10] [20]. The core innovation of DIIS lies in its approach to extrapolation. Instead of using only the most recent Fock matrix to generate the next guess, DIIS constructs a new Fock matrix as a linear combination of all previous Fock matrices in the current iterative subspace [18] [21]. The coefficients for this linear combination are chosen not arbitrarily, but through a constrained minimization procedure that aims to produce an extrapolated Fock matrix with the smallest possible error, thereby driving the SCF procedure toward convergence more rapidly and reliably than simple iteration [11] [19]. This makes it an indispensable component in automated workflows seeking to minimize user intervention and maximize computational efficiency in quantum chemistry studies relevant to drug development.

Mathematical Foundation of DIIS

The DIIS algorithm is built upon a key property of the exact SCF solution: at convergence, the density matrix (P) and the Fock matrix (F) must commute with the overlap matrix (S). This commutator relationship defines the fundamental error metric for the procedure [18] [11].

The Error Vector and Extrapolation

During the SCF cycles, before self-consistency is achieved, a non-zero error vector, ei, can be defined for each iteration _i [18]: ei = S**PiFi - FiP_iS

The central idea of DIIS is to generate an improved guess for the next Fock matrix, F*, as a linear combination of m previous Fock matrices [18] [21]: F* = Σ cj Fj

The coefficients cj_ are determined by minimizing the norm of the corresponding extrapolated error vector, ⟨e*|e*⟩, under the constraint that the coefficients sum to unity (Σ c_j = 1) [18] [21]. This ensures the conservation of the total number of electrons [21].

The DIIS System of Equations

The minimization problem leads to a system of linear equations that can be represented in matrix form [18] [21]:

Where B is a symmetric matrix with elements Bij = ⟨ei | ej⟩, c is the vector of coefficients, and λ is the Lagrange multiplier associated with the constraint Σ cj = 1 [21]. This system is solved using standard linear algebra techniques, such as the LAPACK DGESV routine, to obtain the coefficients _cj_ [21].

DIIS Workflow and Implementation

The DIIS algorithm integrates into the SCF procedure as a sophisticated extrapolation step. The following diagram illustrates the logical workflow and decision points within a typical DIIS-accelerated SCF cycle.

SCF Cycle with DIIS Acceleration

Step-by-Step Protocol

• Initialization: Begin standard SCF iterations. For the first few cycles (e.g., 2-5), proceed without DIIS to build an initial set of Fock and error vectors [20].
• Error Vector Calculation: For iteration i, after constructing the Fock matrix Fi and density matrix Pi, compute the error vector ei = S**PiFi - FiP_iS [18] [21].
• Vector Storage: Store the current Fi and ei. Most implementations limit the number of stored vectors (e.g., 5-15) to manage memory and avoid ill-conditioning of the B matrix. When the subspace is full, older vectors are typically replaced, either by the oldest vector or the one with the largest error norm [18] [21].
• DIIS Extrapolation: Once a sufficient number of vectors (e.g., m ≥ 2) are stored, construct the B matrix and solve the DIIS linear equations to obtain the coefficients cj_ [21].
• Fock Matrix Generation: Form the extrapolated Fock matrix F* = Σ cj Fj [21].
• Orbital Update: Diagonalize F* to obtain a new coefficient matrix, construct a new density matrix, and continue the SCF cycle [21].
• Convergence Check: The SCF procedure is considered converged when the largest element of the latest error vector falls below a predefined cutoff threshold [18].

Convergence Criteria and Thresholds

Convergence in SCF calculations is assessed using multiple criteria to ensure the wavefunction is stable and self-consistent. Different quantum chemistry packages offer predefined levels of convergence stringency, which internally set a group of individual thresholds.

Standard SCF Convergence Criteria

Table 1: Standard SCF convergence criteria and their meanings.

Criterion	Description	Typical Default Value (Single Point)
TolE / SCF_CONVERGENCE	Change in total energy between iterations [11] [22].	10⁻⁵ to 10⁻⁶ E_h [11] [22]
TolErr / DIIS Error	Maximum element of the DIIS error vector (		e		) [18] [22].	10⁻⁵ a.u. [18]
TolMaxP	Maximum change in density matrix elements [22].	10⁻⁵ to 10⁻⁶ [22]
TolRMSP	Root-mean-square change in density matrix elements [22].	10⁻⁶ to 10⁻⁷ [22]

Predefined Convergence Settings in ORCA

Table 2: Comparison of selected convergence criteria (TolE in E_h) for different predefined settings in ORCA [22].

Setting	TolE	TolMaxP	TolRMSP	TolErr	Recommended Use Case
Loose	1 × 10⁻⁵	1 × 10⁻³	1 × 10⁻⁴	5 × 10⁻⁴	Initial geometry steps, large systems
Medium	1 × 10⁻⁶	1 × 10⁻⁵	1 × 10⁻⁶	1 × 10⁻⁵	Standard single-point energies
Tight	1 × 10⁻⁸	1 × 10⁻⁷	5 × 10⁻⁹	5 × 10⁻⁷	Geometry optimizations, frequency analysis [18] [11]
Extreme	1 × 10⁻¹⁴	1 × 10⁻¹⁴	1 × 10⁻¹⁴	1 × 10⁻¹⁴	Benchmarking, high-precision work

For geometry optimizations and subsequent frequency calculations, tighter convergence thresholds (e.g., TightSCF in ORCA or SCF_CONVERGENCE=8 in Q-Chem) are mandatory to ensure accurate and reliable forces and second derivatives [18] [11] [22].

Troubleshooting DIIS Convergence Failures

Despite its power, DIIS can fail or converge slowly. The following table outlines common issues, their diagnostic signatures, and recommended solutions.

Common DIIS Problems and Solutions

Table 3: Troubleshooting guide for DIIS convergence failures in automated SCF protocols.

Problem	Diagnostic Signs	Recommended Solutions
Slow Convergence	Steady but very slow decrease in energy and error.	Increase DIIS_SUBSPACE_SIZE (e.g., from 15 to 25-40) [18] [10]. Use a more robust algorithm like Geometric Direct Minimization (GDM) or TRAH as a fallback [11] [10].
Oscillations	Energy and error norms cycle between values without improving.	Use damping (SlowConv in ORCA) [10]. Reduce the DIIS mixing parameter [6] [20]. Employ level-shifting to separate occupied and virtual orbital energies [10] [19].
Ill-Conditioning	DIIS procedure produces unreasonable coefficients or crashes.	Reset the DIIS subspace (often automatic) [18] [11]. Replace the oldest vector or the vector with the largest error [21].
False Convergence	DIIS error is small, but energy is not converged (e.g., due to error vector cancellation in unrestricted calculations).	Use DIIS_SEPARATE_ERRVEC = TRUE (Q-Chem) to handle alpha and beta error vectors separately [18]. Tighten the energy-based convergence criterion TolE [22].
Pathological Systems	Failure on systems like open-shell transition metals, large clusters, or systems with diffuse basis sets.	Combine SlowConv with a large MaxIter and increased DIISMaxEq [10]. Use electron smearing to treat near-degenerate states [20]. Read in orbitals from a converged, simpler calculation (MORead) [10].

The Scientist's Toolkit: Key Computational Reagents

This section details essential "research reagents" – the key input parameters and algorithms – used to control and fine-tune the DIIS process in automated SCF research.

Essential DIIS Control Parameters

Table 4: Key parameters for controlling DIIS performance in automated SCF convergence.

Parameter/Reagent	Function	Typical Default & Range
DIISSUBSPACESIZE (Q-Chem) / DIISMaxEq (ORCA)	Controls the number of previous Fock/error vectors used for extrapolation [18] [10].	Default: 5-15. Range: 10-40 for difficult cases [18] [10].
Mixing / DIIS%DiMix (ADF/BAND)	The fraction of the new, extrapolated Fock matrix used to update the density for the next cycle. Lower values are more stable [6] [20].	Default: ~0.1-0.2. Range: 0.01-0.3 [6] [20].
SCF_CONVERGENCE (Q-Chem) / TolErr (ORCA)	The convergence threshold for the maximum element of the DIIS error vector [18] [22].	Default (SP): 10⁻⁵ a.u. Tight: 10⁻⁷ to 10⁻⁸ a.u. [18] [22].
LevelShift	Artificially raises the energy of virtual orbitals to reduce occupied-virtual mixing, stabilizing convergence [10] [19].	Value: 0.1 - 0.5 E_h [10].
2-Bromoethane-1-sulfonamide	2-Bromoethane-1-sulfonamide|C2H6BrNO2S	2-Bromoethane-1-sulfonamide (C2H6BrNO2S). A versatile alkyl halide and sulfonamide building block for research. For Research Use Only. Not for human or veterinary use.
4-(Quinazolin-2-yl)phenol	4-(Quinazolin-2-yl)phenol, MF:C14H10N2O, MW:222.24 g/mol	Chemical Reagent

Frequently Asked Questions (FAQ)

Q1: Why does DIIS sometimes converge to a lower energy than expected, and is this desirable? DIIS has a noted tendency to "tunnel" through barriers in wavefunction space, often leading it to the global minimum energy solution rather than a local minimum. This occurs because the density matrix during DIIS iterations is not strictly idempotent until convergence. For most purposes, finding the global minimum is highly desirable, but researchers should be aware that this might bypass a physically expected local minimum [18] [11].

Q2: In an automated geometry optimization, how should SCF convergence criteria be managed? It is often efficient to use a dual-level strategy. In the initial optimization steps, when geometries are poor and forces are large, looser SCF convergence (e.g., LooseSCF) can be used to save time. As the optimization approaches the minimum and forces become small, the criteria should be tightened (e.g., TightSCF) to ensure accurate gradients and a reliable final geometry [22] [6]. Some codes allow this automation within the optimization block [6].

Q3: My calculation is oscillating wildly in the first few iterations. Should I use DIIS immediately? No. Starting DIIS too early can exacerbate initial instabilities. It is recommended to perform a number of initial iterations (e.g., 5-30, controlled by Cyc in ADF) using simple damping or without any acceleration to allow the wavefunction to equilibrate before activating the more aggressive DIIS extrapolation [10] [20].

Q4: What are the main alternatives if DIIS fails completely? Robust fallback algorithms are crucial for automated workflows. Geometric Direct Minimization (GDM) is a highly recommended option that respects the curved geometry of the orbital rotation space [11]. Trust-Region Augmented Hessian (TRAH) or other second-order methods are powerful but more computationally expensive alternatives that can converge pathological cases where DIIS fails [10]. Many modern codes like ORCA can automatically switch to these methods when DIIS struggles [10].

Impact of SCF Stability on Geometry Optimization Pathways and Final Results

This guide examines the critical relationship between Self-Consistent Field (SCF) stability and geometry optimization outcomes. When the SCF procedure fails to converge or produces unstable solutions, it directly compromises the accuracy of calculated energy gradients, leading to flawed optimization pathways and physically meaningless final geometries. Understanding this interplay is fundamental for reliable computational research in drug development and materials science.

Troubleshooting Guides

SCF Convergence Failure: Diagnosis and Solutions

Problem: The SCF procedure fails to converge within the default number of cycles, preventing geometry optimization from proceeding or producing invalid results.

Diagnosis Checklist:

• Monitor Energy Behavior: Examine how the energy changes over the latest iterations. Consistent energy changes in one direction suggest the optimization is progressing but needs more time, while oscillations indicate underlying stability issues [7].
• Check HOMO-LUMO Gap: A small HOMO-LUMO gap (often <0.05 eV) is a primary physical cause of convergence problems, leading to orbital occupation switching or "charge sloshing" [2].
• Verify Initial Guess Quality: Poor initial density guesses, particularly for systems with unusual charge/spin states or metal centers, can prevent convergence [2].
• Inspect Geometry Changes: During optimization, check if bonds are elongating or breaking abnormally, which creates challenging SCF problems [3].

Solution Strategies:

Table: SCF Convergence Solutions and Their Applications

Solution Method	Typical Settings/Values	Applicable Scenarios	Key Considerations
Level Shifting [4]	SCF=vshift=300~500	Small HOMO-LUMO gaps (e.g., transition metal complexes)	Increases virtual orbital energy; doesn't affect final results.
Improved Mixing [6]	SCF%Mixing 0.05, DIIS%Dimix 0.1	Metallic systems, slabs, difficult convergence cases	More conservative mixing stabilizes convergence.
Alternative Algorithms [6]	SCF%Method MultiSecant, DIIS%Variant LISTi	When standard DIIS fails	Different convergence characteristics.
Fermi Broadening [4]	SCF=Fermi	Systems with small band gaps, metallic character	Introduces finite electronic temperature.
Tightened Integration [4]	int=ultrafine, acc2e=12	Calculations with diffuse functions, Minnesota functionals	Higher numerical accuracy at increased computational cost.
Initial Guess Improvement [4]	guess=huckel, guess=read	Problematic initial guesses (e.g., for open-shell systems)	Calculate cation/closed-shell system first for difficult anions/open-shell systems.

Advanced Protocol: For challenging optimizations where the system evolves from a poor to a refined geometry, implement engine automations that dynamically adjust SCF parameters [6]:

This protocol starts with a higher electronic temperature and looser SCF criteria when gradients are large (initial optimization), then tightens them as the geometry approaches convergence.

Geometry Optimization Failure Due to SCF Instability

Problem: Geometry optimization fails to converge or converges to unrealistic structures with artificially short bonds, distorted angles, or incorrect symmetry due to underlying SCF instabilities.

Diagnosis Checklist:

• Verify Gradient Accuracy: Inaccurate forces/energy gradients from poorly converged SCF lead optimization astray [6].
• Check for Numerical Issues: Insufficient integration grids or basis set problems cause numerical noise that corrupts gradients [7] [2].
• Identify Basis Set Problems: Too diffuse basis functions can cause linear dependence; too large frozen cores can cause unrealistically short bonds ("core collapse") [7].
• Monitor Dihedral Angles: Near-180° angles can cause optimizer instability if they develop during optimization (rather than being present initially) [7].

Solution Strategies:

Table: Geometry Optimization Solutions for SCF-Induced Problems

Solution Approach	Implementation Examples	Targeted Problem
Increase Gradient Accuracy [7] [6]	NumericalQuality Good, RadialDefaults NR 10000, SCF converge 1e-8	Noisy gradients from SCF instability
Coordinate System Change [23]	coordsys cartesian (instead of default redundant internals)	Failed optimizations in internal coordinates
Improved Initial Hessian [23]	InHess Almloef, InHess Read (from lower-level calculation)	Poor optimization steps from bad initial guess
Constraint Management [7]	Remove unnecessary constraints or restart optimization	Constraint-induced symmetry breaking
Basis Set Adjustment [7]	Use smaller frozen cores, add confinement, switch to ZORA (relativistic)	Core overlap issues, variational collapse

Advanced Protocol for Organometallic Systems: For period 5/6 metal complexes exhibiting SCF/optimization failures [24]:

• First attempt optimization in gas phase without solvation
• Use smaller basis sets for initial optimization, then guess=read for final calculation [4]
• For solvated systems, gradually introduce solvent model after initial gas-phase optimization
• Consider alternative functionals less prone to convergence issues

Frequently Asked Questions (FAQs)

Q1: My geometry optimization oscillates between two energy values without converging. What does this indicate about SCF stability?

This typically indicates a small HOMO-LUMO gap causing orbital occupation switching [2]. The SCF oscillates between two different orbital occupation patterns, producing different energy landscapes at each geometry step. Solutions include applying level shifting (SCF=vshift=400), using Fermi broadening, or verifying the correct spin state and electronic configuration.

Q2: Why does my optimized structure show unrealistically short bond lengths?

Artificially short bonds often indicate basis set problems exacerbated by SCF issues [7]. With Pauli relativistic methods, this may signal variational collapse (solved by switching to ZORA). Alternatively, large frozen cores that overlap at short distances miss repulsive terms, causing "core collapse." Use smaller frozen cores and ensure sufficient basis set quality.

Q3: How can I distinguish between SCF convergence problems and genuine geometry optimization failures?

Monitor the SCF energy behavior at fixed geometry. If single-point calculations at the current geometry fail to converge, the problem is primarily SCF-related. If SCF converges properly but optimization still fails, examine optimization parameters (coordinate system, constraints, initial Hessian). The workflow below illustrates this diagnostic process.

Q4: My optimization fails specifically when using solvation models. Is this SCF-related?

Yes, solvation models significantly affect the SCF potential [3] [24]. Try converging the SCF in gas phase first, then reading the wavefunction as initial guess for solvated calculation (guess=read) [4]. For PCM calculations, ensure sufficient integration grid quality and verify the solute cavity definition doesn't create numerical instability.

Q5: What SCF stabilization methods are safe for geometry optimization without affecting final results?

Level shifting (SCF=vshift) only affects convergence by raising virtual orbital energies and doesn't alter final converged results [4]. Fermi broadening/finite electronic temperature can be automated to decrease during optimization [6]. Improved initial guesses (guess=read) from simpler calculations provide stability without bias.

Workflow: SCF Stability Management in Geometry Optimization

The following diagram illustrates the systematic approach to diagnosing and resolving SCF-related geometry optimization failures:

The Scientist's Toolkit: Essential Computational Reagents

Table: Key Computational Parameters for Stable SCF-Driven Geometry Optimizations

Computational 'Reagent'	Function/Purpose	Implementation Examples
Level Shifters	Increases HOMO-LUMO gap during SCF to prevent oscillation	SCF=vshift=400 (Gaussian) [4]Electronic temperature automation [6]
Alternative Mixers	Replaces default DIIS for problematic systems	SCF%Method MultiSecant [6]SCF=QC (Quadratic Convergence) [4]
Numerical Stabilizers	Improves integration accuracy for gradients and energy	NumericalQuality Good [7]int=ultrafine [4]
Basis Set Sanitizers	Prevents linear dependence and core overlap issues	Confinement for diffuse functions [6]Smaller frozen cores [7]
Coordinate Transformers	Alternative coordinate systems for stable optimization	coordsys redundant (default) [23]coordsys cartesian (fallback) [23]
Hessian Initializers	Provides better initial optimization direction	InHess Almloef [23]InHess Read (from semiempirical) [23]
Solvation Handlers	Manages solvent model introduction	Gas-phase initial guess → guess=read with solvation [4]Automated convergence criteria [6]
2-Ethoxyoctan-1-amine	2-Ethoxyoctan-1-amine|High-Purity Research Chemical
Cyclobutene, 1-methyl-	Cyclobutene, 1-methyl-, CAS:1489-60-7, MF:C5H8, MW:68.12 g/mol	Chemical Reagent

The interdependence between SCF stability and geometry optimization reliability presents both a challenge and opportunity for automated computational research. By implementing the diagnostic strategies and solution protocols outlined here, researchers can develop more robust computational workflows. Future directions in automated SCF convergence should focus on dynamic parameter adjustment, intelligent fallback strategies, and machine learning-based prediction of optimal method combinations for specific chemical systems.

Advanced Algorithms and Implementation for Automated SCF Workflows

Troubleshooting Guides

FAQ: How do I select the right SCF algorithm for my system?

The optimal SCF algorithm depends heavily on your molecular system and the specific convergence issues you encounter. The table below summarizes the primary characteristics and recommended use cases for each major algorithm.

Table 1: SCF Algorithm Selection Guide

Algorithm	Full Name	Key Principle	Best For	Fallback When
DIIS [11] [25]	Direct Inversion in the Iterative Subspace	Extrapolates new Fock matrices by minimizing the error vector norm ([\mathbf{F}, \mathbf{PS}]) [11].	Default calculations, closed-shell systems [11] [26].	It fails to converge in initial cycles; then try RCA_DIIS or DIIS_GDM [11].
GDM [11]	Geometric Direct Minimization	Takes steps in orbital rotation space that account for its spherical geometry [11].	Restricted open-shell (ROHF) calculations; fallback when DIIS fails [11].	DIIS is oscillating or converging to a high-energy state [11].
SOSCF [25] [26]	Second-Order SCF	Uses an approximate orbital Hessian to achieve superlinear or quadratic convergence [26].	Systems with small HOMO-LUMO gaps, difficult open-shell transition metal complexes [25] [26].	DIIS or GDM are slow or fail to converge tightly.
ADIIS [11] [27]	Accelerated DIIS	An accelerated variant of DIIS; functionally similar to EDIIS for Hartree-Fock [27].	Similar use cases as DIIS; performance can be system-dependent [11] [27].	Standard DIIS is not efficient enough.

The following workflow provides a logical decision path for selecting and troubleshooting SCF algorithms:

FAQ: My calculation involves a transition metal complex. Why does the SCF keep oscillating or diverging?

This is a common problem. Open-shell systems like transition metal complexes have challenging electronic structures with near-degenerate orbitals, which can cause oscillations between different orbital occupancies [26] [22].

Recommended Protocol:

• Initial Guess: Use a better initial guess than the core Hamiltonian. Superposition of Atomic Densities (SAD) or reading orbitals from a previous calculation (init_guess = chkfile in PySCF) can provide a more stable starting point [25].
• Algorithm: Start with GDM (the default for ROHF in Q-Chem) or SOSCF [11] [26]. These methods are more robust for such difficult cases. In ORCA, the TRAH (trust-region augmented Hessian) algorithm is a powerful second-order method [22].
• Advanced Techniques: If oscillations persist, employ the Maximum Overlap Method (MOM). MOM ensures that the calculation occupies a continuous set of orbitals by tracking the overlap with the previous iteration's orbitals, preventing "root flipping" [11].
• Convergence Criteria: For transition metals, using tighter convergence criteria (e.g., !TightSCF in ORCA) is often necessary for accurate geometry optimization and vibrational analysis [11] [22].

FAQ: The SCF energy is changing very slowly in the final cycles and won't meet the convergence threshold. What can I do?

This "trailing convergence" is a common impediment to high-throughput workflows [5].

Recommended Protocol:

• Algorithm Switching: Use a hybrid approach. In Q-Chem, specify SCF_ALGORITHM = DIIS_GDM. This uses the fast DIIS extrapolation initially and switches to the robust Geometric Direct Minimization in later iterations to finalize convergence [11].
• Second-Order Methods: Decorate your SCF object with a second-order solver. In PySCF, this is done with mf = scf.RHF(mol).newton(), which uses the co-iterative augmented hessian (CIAH) method to achieve quadratic convergence near the solution [25].
• Level Shifting: Apply a level shift to increase the energy gap between occupied and virtual orbitals. This stabilizes the SCF procedure. In PySCF, this is controlled by setting the level_shift attribute [25].

FAQ: What are the standard convergence criteria, and when should I tighten them?

SCF convergence is judged based on multiple criteria. The following table outlines standard and tight values, commonly used in programs like ORCA [22].

Table 2: SCF Convergence Criteria Comparison

Criterion	Description	Standard / 'Medium' Value	Tight / 'TightSCF' Value
TolE	Change in total energy between cycles	1e-6 a.u. [22]	1e-8 a.u. [22]
TolRMSP	Root-mean-square change in density matrix	1e-6 [22]	5e-9 [22]
TolMaxP	Maximum change in density matrix	1e-5 [22]	1e-7 [22]
TolErr	DIIS error (maximum element of error vector)	1e-5 a.u. [22]	5e-7 a.u. [22]
TolG	Orbital gradient norm	5e-5 [22]	1e-5 [22]

When to use Tight Criteria:

• Geometry Optimizations and Frequency Calculations: These require tighter thresholds (e.g., SCF_CONVERGENCE = 7 in Q-Chem) to ensure accurate forces and vibrational frequencies [11].
• Transition Metal Complexes: Their complex electronic structure often requires !TightSCF [22].
• Single-Point Energies for High Accuracy: For final energy evaluations, tighter criteria provide more significant figures [11].

The Scientist's Toolkit

This table details key computational "reagents" and their functions in SCF calculations.

Table 3: Essential Research Reagent Solutions for SCF Calculations

Item / Software Feature	Function in Experiment	Example Commands / Usage
DIIS Subspace Size [11]	Controls the number of previous Fock matrices used for extrapolation. A larger subspace can speed up convergence but may become ill-conditioned.	DIIS_SUBSPACE_SIZE = 15 (Q-Chem default) [11]
Level Shifter [25]	Artificially increases the energy gap between occupied and virtual orbitals to stabilize the SCF procedure, useful for systems with small HOMO-LUMO gaps.	mf.level_shift = 0.5 (PySCF) [25]
Damping [25] [28]	Mixes a fraction of the Fock matrix from the previous iteration with the new one to prevent large oscillations in early cycles.	mf.damp = 0.5 mf.diis_start_cycle = 2 (PySCF) [25]
Maximum Overlap Method (MOM) [11]	Prevents oscillations in orbital occupancy by selecting orbitals with the greatest overlap with those from the previous iteration.	MOM is invoked via the STABLE keyword in ORCA or relevant $rem in Q-Chem [11].
Quadratic Converger (QC) [28]	A robust, quadratically convergent algorithm that is slower per cycle but highly reliable for difficult cases. Not available for ROHF.	SCF=QC (Gaussian) [28]
Initial Guess: SAD / 'minao' [25]	Generates the initial density matrix via a superposition of atomic densities, often superior to the core Hamiltonian guess.	mf.init_guess = 'minao' (PySCF default) [25]
Initial Guess: Fragment / 'chk' [25]	Uses the wavefunction from a previous calculation (often a smaller basis set or similar molecule) as a starting point.	mf.init_guess = 'chkfile' mf.chkfile = '/path/to/file' (PySCF) [25]
2,4-Dimethyl-1h-pyrrol-3-ol	2,4-Dimethyl-1H-pyrrol-3-ol	Get 2,4-Dimethyl-1H-pyrrol-3-ol (CAS 1081853-61-3) for your research. This pyrrole building block is For Research Use Only. Not for human or veterinary use.
2,3-Dimethylbut-3-enal	2,3-Dimethylbut-3-enal, CAS:80719-79-5, MF:C6H10O, MW:98.14 g/mol	Chemical Reagent

What is the fundamental principle behind hybrid DIIS-GDM algorithms?

The hybrid DIIS-Geometric Direct Minimization (GDM) algorithm is designed to combine the unique strengths of two powerful Self-Consistent Field (SCF) convergence methods. DIIS (Direct Inversion in the Iterative Subspace) excels at rapidly approaching the global SCF minimum during early iterations, efficiently recovering from initial guesses that may not be close to the final solution [29] [30]. However, DIIS can sometimes struggle to achieve final convergence, particularly when the local energy surface topology becomes challenging [30].

Geometric Direct Minimization (GDM) operates by taking steps in orbital rotation space that properly respect the hyperspherical geometry of the manifold of allowed SCF solutions [29] [31]. Unlike simpler methods that treat this space as flat, GDM accounts for its curved nature, much like how airplanes follow great circle routes rather than straight lines on a map [31]. This geometrical awareness makes GDM extremely robust for final convergence, even if it's slightly less efficient than DIIS for initial steps [29].

The hybrid approach strategically employs DIIS initially to benefit from its rapid approach to the solution basin, then automatically switches to GDM to robustly converge to the precise local minimum [29] [30]. This combination has proven particularly valuable for challenging systems including open-shell molecules and transition metal complexes [30].

Technical Implementation

What are the key control parameters for implementing DIIS-GDM in computational chemistry software?

Successful implementation of the DIIS-GDM hybrid algorithm requires careful configuration of several control parameters. The most critical parameters are summarized in the table below:

Table 1: Key Control Parameters for DIIS-GDM Implementation

Parameter	Default Value	Function	Recommendation
SCF_ALGORITHM	DIIS (varies by package)	Selects the convergence algorithm	Set to DIIS_GDM or DIIS_DM for hybrid approach [29] [30]
MAX_DIIS_CYCLES	50	Maximum DIIS iterations before switching to GDM [29]	Set to 1 for minimal DIIS; higher values (10-30) for difficult cases [29]
THRESH_DIIS_SWITCH	2	Error threshold (10⁻ⁿ) for switching from DIIS to GDM [29]	Values of 2-4 provide balanced performance [29]
SCF_CONVERGENCE	5 (single point), 7 (optimizations)	Convergence criterion (10⁻ⁿ) [30]	Tighter values (7-8) for geometry optimizations [30]
DIIS_SUBSPACE_SIZE	15	Number of previous Fock matrices in DIIS extrapolation [30]	Increase to 25-40 for difficult systems [10]

The switching mechanism between the two algorithms can be triggered by either the DIIS error threshold (THRESH_DIIS_SWITCH) or the maximum number of DIIS cycles (MAX_DIIS_CYCLES), whichever condition is met first [29]. For systems where preserving the initial guess is crucial, setting MAX_DIIS_CYCLES=1 ensures only a single Roothaan step occurs before GDM takes over, providing proper orbital orthogonalization with minimal disturbance to the initial guess [29] [31].

Table 2: Complementary SCF Convergence Parameters

Parameter	Function	Usage Notes
MAX_SCF_CYCLES	Maximum total SCF iterations permitted [30]	Increase to 200-500 for slowly converging systems [10]
DIIS_ERR_RMS	Switches from maximum to RMS error for DIIS [30]	Maximum error typically provides more reliable convergence [30]
Shift / LevelShift	Artificially raises virtual orbital energies [20]	Helps overcome convergence issues but affects properties involving virtual orbitals [20]

Workflow and Process Visualization

What is the complete workflow for the hybrid DIIS-GDM convergence process?

The following diagram illustrates the logical workflow and decision points in the hybrid DIIS-GDM convergence strategy:

The workflow begins with initial guess generation, which is critical for the overall convergence process. The SAD (Superposition of Atomic Densities) guess is compatible with the DIIS_GDM approach, while pure GDM requires an initial guess set of orbitals [29] [31]. The algorithm then proceeds through the DIIS phase, which efficiently reduces the initial large errors and heads toward the solution basin.

The switching condition is continuously monitored during the DIIS phase. When either the DIIS error falls below the threshold defined by THRESH_DIIS_SWITCH (typically 10⁻² to 10⁻⁴) or the number of DIIS cycles reaches MAX_DIIS_CYCLES, the algorithm transitions to the GDM phase [29]. This transition captures the optimal balance between DIIS's efficiency in the initial search and GDM's robustness for final convergence.

Research Reagent Solutions

What essential computational "reagents" are required for implementing hybrid convergence strategies?

Implementing effective hybrid convergence strategies requires both algorithmic components and system-specific adjustments. The table below details key "research reagents" - essential materials and parameters - for successful implementation:

Table 3: Essential Research Reagent Solutions for Hybrid Convergence

Reagent Category	Specific Examples	Function/Purpose	Application Context
Core Algorithms	DIIS (Pulay), GDM, DM, QC [28]	Primary convergence engines	DIIS for initial convergence; GDM for final convergence [29]
Initial Guess Methods	SAD, Core Hamiltonian, Hückel, PModel [10]	Starting point for SCF iterations	SAD guess compatible with DIIS_GDM [29]
Convergence Accelerators	Damping, Level Shifting, Fermi Smearing [20] [28]	Stabilize early SCF iterations	Electron smearing helpful for small HOMO-LUMO gaps [20]
Fallback Strategies	RCA, MOM, TRAH [30] [22]	Alternative approaches when DIIS-GDM struggles	MOM maintains orbital continuity; RCA guarantees energy decrease [30]
System-Specific Templates	SlowConv, VerySlowConv (ORCA) [10]	Pre-configured parameter sets	Transition metal complexes, open-shell systems [10]

These computational reagents must be selected and combined according to the specific chemical system under investigation. For instance, transition metal complexes with localized d-electrons often benefit from stronger damping parameters and delayed second-order convergence steps [10], while systems with very small HOMO-LUMO gaps may require electron smearing to achieve convergence [20].

Troubleshooting Guide

What specific troubleshooting strategies address common DIIS-GDM convergence failures?

Scenario 1: DIIS phase shows wild oscillations or uncontrolled error growth

Problem Identification: The DIIS error (as measured by the commutator ||FD - DF||) fluctuates wildly without establishing a consistent downward trend [20] [10].

Recommended Solutions:

• Implement damping: Reduce the mixing parameter to 0.015-0.09 range to stabilize early iterations [20]
• Increase DIIS subspace size: Expand DIIS_SUBSPACE_SIZE from default 15 to 25-40 to improve extrapolation stability [30] [10]
• Delay DIIS start: Set initial equilibration cycles (Cyc parameter) to 20-30 before DIIS activation [20]
• Switch to RCA initializer: Use RCA_DIIS algorithm for severely problematic cases [30]

Scenario 2: Successful DIIS phase but GDM fails to achieve final convergence

Problem Identification: DIIS reduces error to intermediate levels (10⁻²-10⁻³) but GDM cannot reach tight convergence (10⁻⁶-10⁻⁸).

Recommended Solutions:

• Adjust switch timing: Modify THRESH_DIIS_SWITCH to ensure DIIS doesn't hand over to GDM too early or too late [29]
• Increase maximum iterations: Set MAX_SCF_CYCLES to 200-500 for slowly converging systems [10]
• Verify integral accuracy: Ensure integral threshold (THRESH) is 3-5 orders tighter than SCF_CONVERGENCE [30]
• Enable full Fock rebuilds: Set directresetfreq = 1 to eliminate numerical noise in difficult cases [10]

Scenario 3: Convergence to unphysical or incorrect electronic state

Problem Identification: The algorithm converges efficiently but to an electronic state with incorrect symmetry, occupation, or energy.

Recommended Solutions:

• Verify initial guess and symmetry: Use Guess = PModel or HCore alternatives and disable symmetry if problematic [10] [32]
• Employ Maximum Overlap Method (MOM): Enforce orbital continuity to prevent root flipping [30]
• Converge alternative oxidation state: First converge a closed-shell oxidized/reduced state, then read orbitals as guess [10]
• Perform stability analysis: Check if converged solution represents true minimum or saddle point [22]

Advanced Methodologies

What specialized methodologies exist for pathological cases in automated convergence protocols?

For truly pathological systems that resist standard DIIS-GDM approaches, several advanced methodologies have been developed:

Second-Order Convergence Methods: The Trust Radius Augmented Hessian (TRAH) approach provides robust second-order convergence but at increased computational cost [22]. This method is particularly valuable for systems with multiple nearly-degenerate states. Implementation typically involves automatic activation when standard methods struggle, with control parameters such as AutoTRAHTOl and AutoTRAHIter fine-tuning the activation criteria [22].

Aggressive Damping Protocols: For systems with severe convergence issues, such as metal clusters or complex open-shell species, specialized damping protocols can be implemented:

This configuration, combined with keywords like SlowConv or VerySlowConv in ORCA, provides the heavy damping necessary for pathological cases [10].

Multi-Layer Hybrid Approaches: The most challenging cases may benefit from three-stage convergence strategies:

• Initial stabilization: Heavy damping and delayed DIIS (20-30 cycles)
• Intermediate acceleration: Standard DIIS with expanded subspace (15-25 vectors)
• Final convergence: GDM or quadratically convergent (QC) methods [28]

This multi-stage approach systematically addresses different convergence challenges at appropriate stages of the SCF process.

Frequently Asked Questions

How does the performance of DIIS-GDM compare to other convergence algorithms for transition metal complexes?

For transition metal complexes, particularly open-shell systems, DIIS-GDM typically outperforms pure DIIS while remaining more efficient than pure second-order methods. DIIS alone often struggles with the challenging potential energy surfaces and near-degeneracies common in transition metal systems [10]. Pure GDM, while robust, may require more iterations to approach the solution basin from poor initial guesses [29]. The hybrid approach leverages DIIS to rapidly locate the correct region of the solution space, then employs GDM to reliably converge to the precise minimum, making it particularly well-suited for these chemically important but computationally challenging systems [30].

What are the compatibility constraints between DIIS-GDM and initial guess methods?

The DIIS_GDM hybrid algorithm is compatible with the SAD (Superposition of Atomic Densities) initial guess, while pure GDM requires an initial guess set of orbitals [29] [31]. This compatibility makes the hybrid approach particularly valuable for automated workflows, as it can begin from standard atomic initial guesses without requiring pre-converged orbitals. For difficult cases, initial guesses from lower-level calculations (e.g., BP86/def2-SVP) can be read via MORead functionality to provide improved starting points [10].

How can researchers determine optimal switching parameters between DIIS and GDM?

Optimal switching parameters are system-dependent but can be determined through systematic investigation:

• Begin with defaults: THRESH_DIIS_SWITCH=2 and MAX_DIIS_CYCLES=50 [29]
• Monitor DIIS error progression - switch should occur when error reduction plateaus
• For difficult metals: Use more aggressive DIIS (MAX_DIIS_CYCLES=30-40) before switching
• For stable organic systems: Early switch (MAX_DIIS_CYCLES=10-20) may improve efficiency
• Conservative approach: Set THRESH_DIIS_SWITCH=3 for more DIIS refinement before GDM

What diagnostic tools are available to analyze convergence problems in hybrid algorithms?

Modern computational chemistry packages provide several diagnostic tools:

• SCF iteration reports: Monitor energy changes, density changes, and DIIS error norms [30]
• Orbital gradient analysis: Identify specific orbital pairs causing convergence issues [22]
• Stability analysis: Determine if converged solution represents true minimum [22]
• Density matrix examination: Check for idempotency violations and symmetry breaking [30]
• Convergence threshold monitoring: ORCA's ConvCheckMode provides flexible convergence criteria assessment [22]

These diagnostics enable researchers to identify whether convergence failures occur in the DIIS or GDM phase and apply appropriate corrective strategies.

Frequently Asked Questions (FAQs)

What are the most common causes of SCF convergence failure?

SCF convergence failures typically stem from a few common issues:

• Problematic Molecular Systems: Open-shell systems, transition metal complexes, and diradicals have near-degenerate orbitals that cause charge sloshing [10].
• Inadequate Initial Guess: A poor starting point for the molecular orbitals can lead the SCF procedure down a path to divergence [25].
• Basis Sets with Diffuse Functions: Basis sets like aug-cc-pVDZ can introduce linear dependence in the atomic orbital basis, especially for larger molecules [33].
• Small HOMO-LUMO Gap: Systems with a small energy gap between the highest occupied and lowest unoccupied molecular orbitals are inherently difficult to converge [4] [34].

My calculation converged in one software but not another. Why?

Different quantum chemistry packages often have default settings for SCF convergence algorithms, integration grids, and handling of numerical issues. For instance:

• Linear Dependency Thresholds: The default threshold for removing linearly dependent basis functions varies. Q-Chem and Gaussian use 1e-6, while ORCA uses a tighter 1e-7, which can lead to different behavior with diffuse basis sets [33].
• Default SCF Algorithms: PySCF and ORCA default to DIIS, but ORCA can automatically switch to a more robust Trust Radius Augmented Hessian (TRAH) algorithm if DIIS struggles [10]. Gaussian offers the SCF=QC (quadratic convergence) algorithm as an alternative [4].
• Initial Guesses: The default strategies for generating an initial guess (e.g., 'minao' in PySCF, PModel in ORCA, or core Hamiltonian in Gaussian) can lead the SCF to different solutions or convergence behavior [25] [10].

When should I relax the SCF convergence criteria, and what are the risks?

Relaxing the convergence criteria (e.g., using SCF=conver=6 in Gaussian) can be useful for preliminary geometry optimization steps or single-point energy calculations where high precision in the density matrix is not critical [4].

However, you should avoid relaxed criteria for:

• Final energy calculations where high precision is required.
• Frequency calculations, as the numerical differentiation of gradients is highly sensitive to incomplete SCF convergence and can produce meaningless results [4].
• Property calculations that depend on the virtual orbitals (e.g., excitation energies) if level-shifting techniques are used, as level shifting artificially changes orbital energies [34].

How can I transfer orbitals between calculations to improve convergence?

Transferring a converged wave function from a simpler calculation is a highly effective strategy. Most packages support this:

• PySCF: Use the chkfile initial guess or directly pass a density matrix via the dm0 argument to mf.kernel() [25].
• ORCA: Use the ! MORead keyword and the %moinp "filename.gbw" directive to read orbitals from a previous calculation [10].
• Gaussian: Use guess=read to read a checkpoint file from a previous calculation [4].
• Q-Chem: The gui = 2 option generates a formatted checkpoint file (*.FChk) that can be processed and converted for use in other codes like ORCA [33].

This is particularly useful for converging difficult open-shell systems by first converging a closed-shell cation and using its orbitals as a starting point [4] [10].

Troubleshooting Guides

A Systematic Workflow for SCF Convergence

Follow this logical workflow to diagnose and solve SCF convergence problems. The process is summarized in the diagram below.

Package-Specific Solutions and Settings

This table provides key directives and keywords for implementing common convergence strategies in each software package.

Table 1: SCF Convergence Keywords Across Quantum Chemistry Packages

Convergence Strategy	Q-Chem	ORCA	PySCF	Gaussian
Increase Max Cycles	MAX_SCF_CYCLES = 200	%scf MaxIter 500 end	mf.max_cycle = 200	SCF=maxcyc=200
Improve Initial Guess	scf_guess = gwh	! MORead & %moinp "file.gbw"	mf.init_guess = 'chk' or mf.kernel(dm0=dm)	guess=read
Level Shifting	level_shift = [value]	%scf Shift Shift 0.1 end	mf.level_shift = 0.1	SCF=vshift=300
Damping	scf_damping = [value]	! SlowConv / ! VerySlowConv	mf.damp = 0.5	(Implicit in SlowConv)
Change Algorithm	SCF_ALGORITHM = DIIS_GDM	! KDIIS or ! NoTrah	mf = mf.newton() (SOSCF)	SCF=QC
Handle Linear Dependence	BASIS_LIN_DEP_THRESH = 12	%scf sthresh 1e-6 end	mf = scf.RHF(mol).density_fit()	IOp(3/32=2)

Advanced and System-Specific Protocols

Protocol 1: Converging Open-Shell Transition Metal Complexes

These systems are notoriously difficult due to dense orbital manifolds and near-degeneracies.

• Initial Guess: Start with a broken-symmetry guess from a converged closed-shell ion or use a superposition of atomic potentials (vsap in PySCF) [25] [10].
• Apply Damping: Use strong damping to control charge oscillations. In ORCA, use ! SlowConv or ! VerySlowConv [10]. In PySCF or Q-Chem, set a damping factor of 0.3 to 0.5 [35] [25].
• Algorithm: Disable DIIS initially and use damping-only cycles, or use a second-order method (SOSCF/Newton in PySCF, TRAH in ORCA). For ORCA, combining ! KDIIS with a delayed SOSCFStart can be effective [10].
• Increase DIIS Space: For persistent oscillations, increase the number of DIIS vectors (DIISMaxEq 15 in ORCA, increase DIIS N in ADF) [34] [10].

Protocol 2: Handling Linear Dependence in Diffuse Basis Sets

When using augmented basis sets (e.g., aug-cc-pVXZ) for anions or large molecules.

• Diagnose: Check the output for warnings about the smallest eigenvalue of the overlap matrix and the number of orthogonalized AOs [33].
• Adjust Threshold: The default linear dependence threshold is often 1e-6 (Gaussian, Q-Chem). In ORCA, it is 1e-7 by default; setting it to 1e-6 with sthresh 1e-6 can help [33].
• Force Rebuild: In ORCA, setting directresetfreq 1 ensures a fresh build of the Fock matrix every cycle, eliminating numerical noise that hinders convergence in pathological cases [10].
• Alternative Basis: Consider using a differently-constructed diffuse basis set if linear dependence is severe [33].

The Scientist's Toolkit: Key Research Reagents

This table lists essential "reagents" — computational tools and parameters — for designing robust SCF convergence experiments in automated workflows.

Table 2: Essential Computational Reagents for SCF Convergence

Reagent / Tool	Function in Automated Workflow	Key Considerations
Initial Guess Generators (atom, huckel, chk)	Provides starting electron density. A good guess is crucial for automation.	chk (restart) is most reliable. huckel is a robust alternative for virgin calculations [25].
SCF Accelerators (DIIS)	Speeds up convergence by extrapolating Fock matrices.	Can diverge in difficult cases. May need to be disabled (SCF=noDIIS in Gaussian) or tuned (increase DIISMaxEq) [4] [10].
Second-Order Convergers (SOSCF, TRAH)	Provides robust, quadratic convergence near the solution.	More computationally expensive per iteration but more reliable. ORCA's TRAH activates automatically [10].
Stabilizers (Damping, Level Shift)	Suppresses oscillations in the iterative process.	Level shifting (SCF=vshift=300) is highly effective for small-gap systems [4] [34].
Linear Dependency Threshold	Removes numerically redundant basis functions.	Critical for automation with diffuse basis sets. A value of 1e-6 is a standard default [33].
Integration Grid (DFT)	Defines numerical accuracy for XC integration.	Too coarse a grid can cause convergence failure. For Minnesota functionals, use a fine grid (int=ultrafine in Gaussian) [4].
Fractional Occupancy Smearing	Helps converge metallic systems and small-gap systems by populating orbitals near the Fermi level.	Introduces a fictitious electronic temperature. Energy must be extrapolated to 0 K [25] [34].
2,2-Dimethylpiperidin-3-ol	2,2-Dimethylpiperidin-3-ol
(8-Bromooctyl)cyclopropane	(8-Bromooctyl)cyclopropane

Experimental Protocols for Robust Geometry Optimization

Protocol 1: Two-Layered SCF Convergence for Geometry Optimization

This protocol ensures computational efficiency while maintaining reliability during geometry optimizations.

• Initial Optimization Phase:

  • Use a looser SCF convergence threshold (e.g., SCF=conver=6 in Gaussian) and a moderate integration grid.
  • Use a smaller basis set (e.g., def2-SVP) if appropriate for the chemical problem.
  • The goal is to efficiently relax the geometry to a reasonable starting point for the final refinement.

• Final Optimization Phase:

  • Use the optimized geometry from the first phase.
  • Switch to the target, higher-level theory (e.g., larger basis set, hybrid functional).
  • Enforce tight SCF convergence (default or tighter) and a fine integration grid.
  • Use the wave function from the first phase as the initial guess (guess=read).

Protocol 2: Stability Analysis for Confirming the True Ground State

A converged SCF solution is not guaranteed to be the ground state; it might be a saddle point. Always perform a stability test after optimizing a challenging molecule, especially if it is suspected to be diradicaloid or has open-shell character [25].

• Run a Stability Analysis: This perturbs the wave function and checks if it can collapse to a lower-energy state.

  • PySCF: Use the mf.stability() function explicitly after the SCF [25].
  • ORCA/Gaussian: Use specific keywords (! Stable in ORCA, stable in Gaussian) in the input file.

• Follow-Up:

  • If the wave function is unstable, take the lowered-energy solution from the stability analysis and re-optimize the geometry, as the new state might have a different optimal structure.

Troubleshooting Guides

Guide 1: Addressing SCF Oscillations with Damping and DIIS

Problem: The Self-Consistent Field (SCF) procedure exhibits non-convergent oscillatory behavior, cycling between values without reaching convergence.

Explanation: Oscillations often occur when the new electron density creates a potential that causes large, unstable shifts in the subsequent electron density. Simple damping controls this by mixing the new Fock matrix with that from the previous cycle [34].

Solution: The default ADIIS+SDIIS acceleration method is usually effective. If oscillations persist, adjust the damping or DIIS parameters.

Method	Key Command / Parameter	Function	Default Value	Recommended Adjustment for Oscillations
Simple Damping	Mixing mix	Sets mixing parameter for Fock matrices: F_new = mix * F_n + (1-mix) * F_{n-1} [34].	0.2 [34]	Increase to 0.3-0.5 to stabilize slow, steady convergence [34].
DIIS Vector Number	DIIS N n	Number of previous cycles used in the DIIS linear combination [34].	10 [34]	For small systems, try decreasing. For large/complex systems, increase to 12-20 [34].
SDIIS Start	NoADIIS + DIIS OK ok	Disables ADIIS; SDIIS starts when commutator error falls below ok [34].	0.5 a.u. [34]	Use NoADIIS and lower the OK threshold if ADIIS is unstable [34].

Experimental Protocol:

• Begin with default SCF settings.
• If oscillations occur after ~10 cycles, increase the Mixing parameter.
• If the system is large and oscillations persist, increase the DIIS N parameter.
• For persistent issues in the initial stages, use the NoADIIS keyword to revert to the more stable damping+SDIIS scheme [34].

Guide 2: Correcting for Charge Sloshing with Level Shifting

Problem: Charge sloshes back and forth between orbitals that are close in energy near the Fermi level.

Explanation: Level shifting raises the energy of the virtual (unoccupied) orbitals, making it energetically unfavorable for electrons to jump into them during the SCF process, which helps stabilize convergence [34] [36].

Solution: Enable level shifting. Note that this method is only available in the OldSCF module and is not suitable for properties calculations that involve virtual orbitals [34].

Parameter	Key Command	Function	Typical Value
Shift Value	Lshift vshift	Raises diagonal Fock matrix elements for virtual orbitals by vshift Hartree [34].	0.5 - 1.0 Hartree [34]
Deactivation Error	Lshift_err shift_err	Level shifting turns off when SCF error drops below this threshold [34].	0.1
Activation Cycle	Lshift_cyc shift_cyc	Level shifting is not activated before this SCF cycle [34].	1

Experimental Protocol:

• Activate the old SCF procedure with the OldSCF keyword [34].
• Use the Lshift key with a value between 0.5 and 1.0.
• To minimize interference with the final converged state, set Lshift_err to automatically disable shifting near convergence [34].

Guide 3: Handling Metallic Systems and Small-Gap Cases with Fermi Smearing

Problem: SCF convergence fails for systems with a small or no HOMO-LUMO gap, such as metals or molecules with nearly degenerate frontier orbitals.

Explanation: Fermi smearing (or fractional occupation) assigns partial occupations to orbitals around the Fermi level according to a temperature-dependent distribution. This prevents large changes in orbital occupancy from small shifts in orbital energy, smoothing the convergence path [36].

Solution: Apply electron smearing to partially occupy orbitals near the Fermi level. This technique is particularly effective for metallic systems with no band gap [36].

Experimental Protocol:

• Identify systems with known small HOMO-LUMO gaps or metallic character.
• Enable the Occupations key with a smearing function (e.g., Fermi).
• Set an initial temperature parameter to define the width of the smearing.
• The smearing can be annealed (gradually reduced) as the SCF procedure approaches convergence [36].

Frequently Asked Questions (FAQs)

Q1: The SCF cycles are not converging. What is my systematic first-step approach? Begin by verifying the quality of your initial guess for the electron density. Then, confirm that your system has a correct electronic state and a sensible geometry. For difficult cases, the MESA acceleration method can be invoked, which intelligently combines multiple algorithms (ADIIS, fDIIS, LISTb, LISTf, LISTi, SDIIS) to find one that works [34].

Q2: When should I use the older OldSCF procedure instead of the default one? The new default SCF is recommended for most cases. However, OldSCF is automatically enabled or required if you use specific keywords like Occupations Steep, Lshift (level shifting), ARH, EDIIS, or RESTOCC [34].

Q3: What does the SCF convergence criterion actually mean? The primary criterion is based on the maximum element of the commutator of the Fock (F) and density (P) matrices, [F,P]. This commutator is zero at perfect self-consistency. Convergence is achieved when this maximum element is below your set SCFcnv value (default is 1e-6) [34].

Q4: My geometry optimization is failing due to SCF issues. Are there alternative strategies? Yes, integrating advanced geometry optimization algorithms with robust energy potentials can side-step SCF problems. For instance, the conjugate gradient with backtracking line search (CG-BS) algorithm combined with the machine learning potential ANI-2x can optimize structures without direct SCF cycles, improving docking and scoring power in drug discovery applications [37]. In molecular dynamics, the Car-Parrinello Monitor (CPMonitor) can detect SCF failures and switch to a Car-Parrinello MD (CPMD) Hamiltonian to propagate through problematic regions before switching back to BOMD [36].

The Scientist's Toolkit: Research Reagent Solutions

Essential Material / Algorithm	Function in Automated Convergence
DIIS (Direct Inversion in Iterative Subspace)	An acceleration method that uses a linear combination of Fock matrices from previous iterations to generate a better guess for the next iteration [34] [38].
ADIIS (Augmented DIIS)	A variant of DIIS that uses an augmented Roothaan-Hall energy function to determine the linear coefficients, often combined with standard Pulay DIIS (SDIIS) for robustness [34] [38].
LIST (LInear-expansion Shooting Technique)	A family of SCF acceleration methods developed by Y.A. Wang's group, considered a generalization of damping [34].
MESA Method	A meta-algorithm that dynamically combines multiple acceleration methods (ADIIS, fDIIS, LISTb, LISTf, LISTi, SDIIS) to achieve convergence where individual methods fail [34].
ANI-2x Potential	A machine learning potential that provides highly accurate molecular energy predictions, resembling wB97X/6-31G(d) model chemistry. It can be used with the CG-BS optimizer for geometry optimization, bypassing traditional SCF convergence issues [37].
CG-BS (Conjugate Gradient with Backtracking Line Search)	A geometry optimization algorithm that uses previous movement directions and Wolfe conditions for efficient iteration. It is particularly effective when combined with the ANI-2x potential [37].
CPMonitor (Car-Parrinello Monitor)	A method for BOMD simulations that detects SCF convergence failures and switches to Car-Parrinello MD to propagate through problematic configuration space, then switches back to BOMD [36].
(2S,3S)-3-aminopentan-2-ol	(2S,3S)-3-aminopentan-2-ol, MF:C5H13NO, MW:103.16 g/mol
N-ethyl-2-iodoaniline	N-ethyl-2-iodoaniline, MF:C8H10IN, MW:247.08 g/mol

Workflow and Relationship Diagrams

Specialized Techniques for Open-Shell Systems and Transition Metal Complexes

Frequently Asked Questions

What are the most common physical reasons an SCF calculation fails to converge? SCF convergence failures often stem from the electronic structure itself [2]. Common physical reasons include:

• Small or zero HOMO-LUMO gap: This can cause repetitive changes in frontier orbital occupation numbers or oscillations in the orbital shapes (known as "charge sloshing"), where a small error in the Kohn-Sham potential leads to a large density distortion [2].
• Poor initial guess: Starting from a poor initial electron density, especially for systems with unusual charge/spin states or metal centers, can hinder convergence from the beginning [2].
• Incorrect system setup: Using an incorrect molecular geometry (e.g., unrealistic bond lengths), charge, or spin multiplicity makes convergence difficult [10] [20].

Why are open-shell transition metal complexes particularly challenging? Transition metal complexes, especially open-shell species, are difficult because their electronic structure often involves complex open-shell states, localized unpaired electrons, and near-degenerate configurations that lead to multiple possible spin couplings [39]. The Hartree-Fock method is a poor starting point, plagued by instabilities [39].

My calculation is oscillating wildly in the first few iterations. What should I do? Wild oscillations at the start of the SCF procedure often indicate a poor initial guess or a system that requires damping. Recommended actions include [10]:

• Applying damping through keywords like SlowConv or VerySlowConv.
• Using level-shifting techniques to stabilize the initial cycles.
• Trying a simpler method or basis set to generate a better initial guess (e.g., BP86/def2-SVP), then reading those orbitals into the more complex calculation using MORead [10].

The SCF was almost converged but ran out of iterations. How can I fix this? If the SCF shows steady convergence but hits the iteration limit, the simplest solution is to increase the maximum number of SCF cycles [10]. You can then restart the calculation from the last set of orbitals to continue the process.

What does it mean if my calculation has "near SCF convergence"? ORCA defines "near convergence" as a state where the energy change and density changes are below specific thresholds but not all convergence criteria are fully met [10]. By default, ORCA will stop single-point calculations in this state but may continue in a geometry optimization, reusing the orbitals as a guess for the next cycle [10]. You should always check if results from such calculations are reliable for your purposes.

Troubleshooting Guides

Guide 1: Systematic Approach to SCF Convergence Problems

Follow this logical workflow to diagnose and resolve SCF convergence issues.

Step 1: Verify the Fundamental Setup

Before adjusting complex parameters, check the basics.

• Geometry: Ensure atomic coordinates are realistic and in the correct units (typically Ã…ngströms) [20]. Overly long/short bonds can cause small HOMO-LUMO gaps or linear dependence [2].
• Charge and Multiplicity: Confirm the system's total charge and spin multiplicity are correct. For open-shell transition metals, this is critical [40].

Step 2: Improve the Initial Orbital Guess

A better starting point can resolve many convergence issues.

• Use a simpler calculation: Converge a calculation with a smaller basis set (e.g., def2-SVP) or a simpler functional (e.g., BP86). Use the resulting orbitals as a guess for the target calculation via ! MORead [10].
• Alternative guess generators: Try PAtom, Hueckel, or HCore instead of the default PModel guess [10].
• Converge a closed-shell analogue: For an open-shell system, try converging a closed-shell cation/anion and use its orbitals as the guess [10].

Step 3: Adjust SCF Algorithm and Parameters

If a better guess doesn't work, modify the SCF procedure.

• For trailing convergence: If convergence slows near the end, enable the Second-Order SCF (SOSCF) method with ! SOSCF. For open-shell systems, you might need to delay its start with SOSCFStart 0.00033 [10].
• For oscillations: Use damping (! SlowConv) or level-shifting (%scf Shift 0.1 end) [10]. Alternatively, use the KDIIS algorithm (! KDIIS) [10].
• Let the program handle it: Modern ORCA uses the robust Trust Radius Augmented Hessian (TRAH) algorithm automatically if the default DIIS struggles. You can adjust its activation threshold with AutoTRAHTOl [10].

Step 4: Advanced Techniques for Pathological Cases

For truly difficult systems (e.g., metal clusters), more expensive settings may be necessary [10].

• Increase DIIS subspace: Set DIISMaxEq 15 (or even up to 40) to use more Fock matrices in the DIIS extrapolation.
• Reduce numerical noise: Set directresetfreq 1 to rebuild the Fock matrix fully in every iteration, eliminating integration inaccuracies that hinder convergence.
• Greatly increase iterations: Set MaxIter 1500 for systems requiring hundreds of cycles.

Guide 2: Converging Pathological Open-Shell Systems

This protocol is specifically for difficult open-shell transition metal complexes and radicals [10].

Detailed Methodology:

• Initial Attempt: Use a combination of damping and the KDIIS algorithm.
  The SlowConv keyword applies damping to control large initial fluctuations, while KDIIS with SOSCF can provide faster convergence once near the solution [10].

• Handle SOSCF Instability: If the SOSCF step fails with warnings about "huge, unreliable steps," disable it or make it more conservative.

  • Disable SOSCF: ! NOSOSCF
  • Delay SOSCF start: %scf SOSCFStart 0.00033 end (reduces the default gradient threshold by a factor of 10) [10].

• Final Resort - Expensive but Robust Settings: If other methods fail, use these settings to maximize stability.

  These settings increase computational cost but are often the only way to converge systems like iron-sulfur clusters [10].

Research Reagent Solutions

The table below summarizes key techniques and their functions for troubleshooting SCF convergence.

Technique/Keyword	Primary Function	Typical Use Case
SlowConv / VerySlowConv [10]	Applies damping to the SCF procedure.	Wild oscillations in early SCF cycles.
SOSCF [10]	Activates second-order convergence algorithm.	"Trailing" convergence near the solution.
KDIIS [10]	Uses a different (KDIIS) SCF algorithm.	Systems where standard DIIS performs poorly.
MORead [10]	Reads orbitals from a previous calculation.	Providing a high-quality initial guess.
Level Shifting [10] [20]	Artificially raises energy of virtual orbitals.	Stabilizing convergence in difficult cases.
Electron Smearing [20]	Uses fractional orbital occupations.	Systems with a very small HOMO-LUMO gap (e.g., metals).
TRAH [10]	Activates robust trust-region algorithm.	Default fallback in ORCA when DIIS struggles.

SCF Convergence Tolerance Settings

The table below shows selected convergence criteria for ORCA. Using tighter tolerances requires more SCF cycles but yields more accurate results [22].

Criterion	LooseSCF	NormalSCF (default)	TightSCF
TolE (Energy Change)	1e-5	1e-6	1e-8
TolMaxP (Max Density Change)	1e-3	1e-5	1e-7
TolRMSP (RMS Density Change)	1e-4	1e-6	5e-9
TolErr (DIIS Error)	5e-4	1e-5	5e-7
Recommended For	Preliminary tests, population analysis.	Most standard calculations.	High-accuracy work, transition metals, property calculations.

Why does my geometry optimization fail to converge or run too slowly?

Geometry optimization may fail to converge or be inefficient due to a combination of factors related to your choice of optimizer, coordinate system, and the quality of your initial structure and computed forces.

• Optimizer and Coordinate System: The choice of optimizer and whether it uses internal coordinates (e.g., bonds, angles) or Cartesian coordinates is crucial. A 2023 benchmark study found that internal coordinates generally require fewer steps to reach an equilibrium structure than Cartesian coordinates [41]. Some optimizers, like Sella and geomeTRIC, are designed to leverage internal coordinates [42].
• Initial Geometry and Hessian: Starting far from the minimum energy structure can slow convergence. The choice of the initial Hessian (a matrix of second derivatives) and the method used to update it during quasi-Newton optimization significantly impacts the convergence rate [41].
• Force Accuracy: The success of optimization depends on the accuracy of the calculated forces (energy gradients). Inaccurate forces, often stemming from insufficient SCF convergence or low-quality numerical settings, can misguide the optimizer [7].

How do I configure an optimizer to use internal coordinates for better performance?

Configuring an optimizer to use internal coordinates can significantly enhance performance. Below is a comparison of common open-source optimizers and their use of coordinate systems, based on a benchmark with neural network potentials (NNPs) and quantum chemical methods [42] [41].

Optimizer	Primary Coordinate System	Key Features	Performance Notes
Sella	Internal	Uses rational function optimization; suited for minima & transition states [42].	Fast convergence; high success rate in benchmarks [42] [41].
geomeTRIC	Internal (TRIC)	Employs Translation-Rotation Internal Coordinates (TRIC) with L-BFGS [42].	Performance varies; can be highly efficient with compatible NNP [42].
ASE/L-BFGS	Cartesian	A classic quasi-Newton method [42].	Robust but often requires more steps than internal coordinate methods [42] [41].
ASE/FIRE	Cartesian	First-order, dynamics-based, noise-tolerant [42].	Can be fast but may be less precise for complex systems [42].

The workflow for selecting and applying an optimizer can be summarized as follows:

What quantitative performance gains can I expect from using internal coordinates?

The performance gain from using internal coordinates is clearly demonstrated in benchmarks. The following table summarizes results from a study optimizing 25 drug-like molecules with different Neural Network Potentials (NNPs), showing the average number of steps required by different optimizers [42].

Optimizer	OrbMol NNP	OMol25 eSEN NNP	AIMNet2 NNP	Egret-1 NNP	GFN2-xTB (Control)
Sella (internal)	23.3	14.9	1.2	16.0	13.8
ASE/L-BFGS (Cartesian)	108.8	99.9	1.2	112.2	120.0
ASE/FIRE (Cartesian)	109.4	105.0	1.5	112.6	159.3
geomeTRIC (tric)	11.0	114.1	49.7	13.0	103.5

Beyond speed, the choice of optimizer and coordinate system affects the quality of the final structure. A good optimization should find a true local minimum (with zero imaginary frequencies). The same study reported how many of the 25 optimized structures were true minima [42]:

Optimizer	OrbMol	OMol25 eSEN	AIMNet2	Egret-1	GFN2-xTB
Sella (internal)	15	24	21	17	23
ASE/L-BFGS (Cartesian)	16	16	21	18	20
geomeTRIC (cart)	6	8	22	5	7

What is a detailed experimental protocol for benchmarking optimizer performance?

To reliably benchmark geometry optimizers in your own automated workflow, follow this detailed protocol.

Objective: Compare the performance and reliability of different geometry optimization algorithms when integrated with your chosen energy and gradient calculator (e.g., a Quantum Chemistry software or an NNP).

Materials and Setup:

• Test Set: Select a diverse set of molecular structures. A recommended starting point is 25 drug-like molecules, as used in recent benchmarks [42]. Ensure the structures are available in a consistent format (e.g., XYZ).
• Computational Method: Choose the method for calculating energies and forces (e.g., a specific NNP like OrbMol or AIMNet2, or a DFT functional and basis set).
• Optimizers: Select at least two optimizers for comparison, ideally one using internal coordinates (e.g., Sella, geomeTRIC) and one using Cartesian coordinates (e.g., ASE/L-BFGS).
• Convergence Criteria: Define a strict and consistent convergence criterion. A common choice is a maximum force component (fmax) below 0.01 eV/Ã…, with a maximum step limit of 250 steps to identify non-converging cases [42].
• Computational Environment: Use a consistent software environment (e.g., Python with ASE, Sella, and geomeTRIC libraries) and hardware to ensure fair comparisons.

Procedure:

• Initialization: For each molecule in the test set, generate a starting geometry that is perturbed from a known stable conformation.
• Optimization Execution: For each optimizer, run the geometry optimization using the chosen computational method and the predefined convergence criteria.
• Data Collection: For each run, record:
  • Success/Failure: Whether the optimization converged within the step limit.
  • Steps to Converge: The number of steps taken for successful runs.
  • Final Energy and Forces: The energy and maximum force at the final geometry.
• Post-Processing Analysis:
  • Frequency Calculations: Perform a vibrational frequency calculation on each successfully optimized structure to determine if it is a true local minimum (zero imaginary frequencies) [42].
  • Data Aggregation: Calculate the average number of steps, success rate, and the percentage of structures that optimized to true minima for each optimizer.

The Scientist's Toolkit: Key Research Reagents

Item	Function in Experiment
Baker Test Set	A standard set of 30 organic molecules used for validating and benchmarking optimization algorithms [41].
Neural Network Potentials (NNPs)	Machine-learned potentials (e.g., OrbMol, AIMNet2) that provide DFT-level accuracy at a fraction of the cost for energy and force calculations [42].
Atomic Simulation Environment (ASE)	A Python library that provides a unified interface to numerous optimizers (FIRE, L-BFGS) and atomistic simulation codes [42].
Sella & geomeTRIC	Specialized optimization packages that implement advanced internal coordinate schemes for efficient convergence to minima or transition states [42].
Vibrational Frequency Code	A post-processing tool to confirm optimized structures are true local minima by checking for the absence of imaginary frequencies [42].

Troubleshooting FAQs

Q: My optimization is oscillating and will not converge. What should I do? A: First, check how the energy changes over the last iterations. If it's steadily changing, simply increasing the maximum number of iterations may help. If the energy is oscillating, the problem may lie in the accuracy of the calculated forces. Try the following:

• Increase numerical accuracy: Use a higher-quality numerical integration grid or a larger basis set [7].
• Tighten SCF convergence: Use a stricter SCF convergence criterion (e.g., 1e-8 instead of 1e-6) to ensure gradient accuracy [7].
• Change coordinates: Switch from Cartesian to delocalized internal coordinates, as they are generally more efficient and stable [7].

Q: The optimized structure has imaginary frequencies. What does this mean and how can I fix it? A: Imaginary frequencies indicate the optimization converged to a saddle point, not a minimum. This is a common issue, with some optimizer/NNP combinations producing a significant number of such structures [42].

• Continue optimization: You can often restart the optimization from the saddle point structure, and the optimizer may find the nearby minimum.
• Use a different optimizer: Benchmarks show that some optimizers, particularly those using internal coordinates like Sella (internal), are much more effective at finding true minima than others [42].
• Check initial guess: An poor initial geometry can lead the optimizer down a path to an incorrect saddle point.

Q: My SCF calculations fail to converge during the optimization. How can I resolve this? A: SCF non-convergence is a common problem, especially for systems with small HOMO-LUMO gaps or open-shell transition metals.

• Improve the initial guess: Use a better initial guess (e.g., PAtom or HCore in ORCA) or read in orbitals from a converged, simpler calculation [10].
• Use damping or level shifting: Employ keywords like SlowConv or manually set a level shift (e.g., 0.1 Hartree) to dampen oscillations in the initial SCF iterations [10].
• Adjust the DIIS space: For difficult cases, increasing the number of DIIS expansion vectors (DIISMaxEq in ORCA) to 15-40 can help, though this is more expensive [10].
• Enable robust convergers: In modern codes like ORCA, allow robust second-order convergers like TRAH (Trust Radius Augmented Hessian) to activate automatically if the standard DIIS fails [10].

Systematic Protocols for Diagnosing and Resolving SCF Convergence Failures

Frequently Asked Questions

• What defines SCF convergence? Convergence is typically determined by thresholds (tolerances) set for the change in total energy between iterations (TolE), the root-mean-square change in the density matrix (TolRMSP), and the maximum element change in the density matrix (TolMaxP). The calculation is considered converged when all specified criteria fall below their thresholds [43].

• Why does my calculation oscillate between two energy values? This is a classic sign of SCF oscillation, often caused by an overly aggressive DIIS algorithm or an insufficiently damped initial guess in systems with a small HOMO-LUMO gap. It is common in metallic systems, clusters, and molecules with diffuse basis functions [10] [25].

• My calculation is converging, but is taking hundreds of iterations. What can I do? This is slow convergence, which frequently occurs in open-shell transition metal complexes and systems with near-degeneracies. The cause is often a poor initial guess for the molecular orbitals or a suboptimal SCF algorithm for the system's electronic structure [10].

• The calculation says it converged, but the energy is much higher than expected. What happened? This may be a case of false convergence, where the SCF procedure has converged to an excited state or a saddle point on the electronic energy surface rather than the true ground state. This necessitates a stability analysis to check if the solution is stable [25].

• How does the choice of basis set affect SCF convergence? Large basis sets with diffuse functions (e.g., aug-cc-pVTZ) can introduce linear dependencies, making the SCF problem more ill-conditioned and harder to converge [10].

---

Troubleshooting Guides

This section provides a structured methodology for diagnosing and resolving common SCF failure patterns, framed within automated convergence research.

Oscillation

Diagnosis: The SCF energy oscillates between two or more values without settling. Monitor the "Delta E" and "RMS |[F,P]|" in the output [44].

Resolution Strategies:

• Enable Damping: Introduce damping by mixing a portion of the old Fock matrix with the new one. This stabilizes the initial iterations [25].

• Adjust Mixing Parameters: Reduce the mixing parameter (mixing, AMIX in VASP) to take smaller steps in the electronic update [45]. For heterogeneous systems like surfaces or oxides, switching to a local mixing mode like 'local-TF' can be essential [45].
• Use a Robust Algorithm: Switch from the default DIIS to a second-order convergence (SOSCF) or Trust Radius Augmented Hessian (TRAH) algorithm, which are more stable for pathological cases [10].
• Increase DIIS Space: For difficult systems, increasing the number of Fock matrices stored for the DIIS extrapolation (DIISMaxEq) can help break oscillatory patterns [10].

Table: Quantitative Damping and Mixing Parameters Across Codes

Code	Parameter/Block	Function	Recommended Value for Oscillation
ORCA	! SlowConv	Keyword activating larger damping	N/A [10]
PySCF	damp factor	Damping factor for Fock matrix	0.5 - 0.8 [25]
ASE-QE	convergence['mixing']	Mixing parameter for charge density	0.1 - 0.3 [45]
VASP	BMIX, AMIX	Mixing parameters for the charge density	Reduce significantly [45]

Slow Convergence

Diagnosis: The energy and density metrics decrease monotonically but at an extremely slow rate, often failing to converge within the default maximum number of iterations.

Resolution Strategies:

• Improve the Initial Guess: The default superposition of atomic densities (SAD) guess is good, but for difficult systems, a better guess is crucial.
  • Read Checkpoint File: Use orbitals from a previous, simpler calculation (e.g., a smaller basis set or a different charge/spin state) as the initial guess [10] [25].
  • Hückel Guess: Employ a parameter-free Hückel guess, which can be more reliable than the core Hamiltonian guess [25].
• Switch SCF Algorithm: For open-shell systems, the KDIIS algorithm, sometimes combined with SOSCF, can lead to faster convergence than standard DIIS [10].
• Increase Maximum Iterations: Simply increasing the maximum number of SCF cycles can allow a slowly converging calculation to finish [10] [46].

• Adjust Integral Grids: In rare cases, an insufficiently accurate integration grid (for DFT) can cause slow convergence. Increasing the grid size can help [10].

Table: Advanced SCF Algorithm Settings for Slow Convergence

Algorithm	Code	Typical Use Case	Key Tuning Parameter
SOSCF	ORCA, PySCF	Speeds up convergence once a threshold is reached	SOSCFStart (reduce for TMs) [10]
TRAH	ORCA	Robust second-order converger for difficult cases	AutoTRAHTOl [10]
KDIIS+SOSCF	ORCA	Alternative for open-shell and TM systems	SOSCFStart [10]
Newton solver	PySCF	Second-order method for quadratic convergence	.newton() decorator [25]

False Convergence

Diagnosis: The SCF procedure reports convergence based on the specified thresholds, but the resulting energy is unphysically high, or the electron density appears incorrect.

Resolution Strategies:

• Perform Stability Analysis: This is the most critical step. A stability analysis checks if the converged wavefunction is a true minimum or if it can collapse to a lower-energy state [25].
  • Internal Stability: Checks for lower-energy solutions within the same symmetry/restriction (e.g., RHF → RHF).
  • External Stability: Checks for lower-energy solutions by breaking symmetry or restrictions (e.g., RHF → UHF). If an instability is found, the calculation should be restarted using the unstable solution as a new guess.
• Tighten Convergence Criteria: Using tighter thresholds (e.g., !TightSCF in ORCA) ensures the density is fully converged before proceeding, preventing premature convergence [43].
• Use Level Shifting: Applying a level shift artificially increases the energy gap between occupied and virtual orbitals, which can help avoid convergence to saddle points and stabilize the procedure [25].

• Try Fractional Occupations/Smearing: For systems with a small or zero HOMO-LUMO gap (e.g., metals), using fractional orbital occupations via electronic temperature smearing can prevent the SCF from getting stuck [25] [46].

Table: Standard vs. Tight SCF Convergence Tolerances (ORCA) [43]

Criterion	Description	!StrongSCF (Typical)	!TightSCF
TolE	Energy change	3e-7 Eh	1e-8 Eh
TolRMSP	RMS density change	1e-7	5e-9
TolMaxP	Max density change	3e-6	1e-7
TolErr	DIIS error	3e-6	5e-7

The Scientist's Toolkit: Essential SCF Parameters

Table: Key Research Reagents for SCF Convergence

Item	Function in SCF "Experiment"
Initial Guess (SAD, Hückel, Core)	The starting point for the electronic density, critically influencing convergence speed and path [25] [44].
DIIS (Direct Inversion in Iterative Subspace)	An extrapolation algorithm that accelerates convergence by using information from previous iterations [10] [25].
Damping Factor	A numerical "stabilizer" that mixes old and new Fock/density matrices to dampen oscillations [25].
Level Shift	An energy "spacer" applied to virtual orbitals to stabilize the SCF procedure and avoid saddle points [25].
Smearing/Electronic Temperature	A tool to assign fractional orbital occupations, essential for converging metallic systems with degenerate states [25] [46].
SCF Stability Analysis	A diagnostic "assay" to determine if a converged wavefunction is a true ground state or an unstable solution [25].
2-(2-Pyrazinyl)-2-propanol	2-(2-Pyrazinyl)-2-propanol
4-Bromo-3-ethynylphenol	4-Bromo-3-ethynylphenol|Supplier

Experimental Protocol: Automated SCF Convergence Workflow

The following diagram illustrates a logical workflow for diagnosing and treating SCF failures, suitable for integration into an automated geometry optimization research protocol.

Frequently Asked Questions

1. My SCF calculation fails to converge. What are the first things I should check? Start with the most fundamental aspects of your calculation. First, ensure your molecular geometry is physically realistic, checking that bond lengths and angles are reasonable and that no atoms are missing from your input structure [20]. Second, confirm that you have correctly specified the system's spin multiplicity; open-shell systems often require an unrestricted calculation formalism [20]. Finally, verify that you are using an appropriate initial guess. For difficult cases, reading in orbitals from a simpler, pre-converged calculation (e.g., using a smaller basis set or functional) can provide a better starting point [10].

2. Which types of chemical systems are most prone to SCF convergence problems? Convergence issues are frequently encountered in systems with specific electronic structures [20] [10]:

• Systems with small HOMO-LUMO gaps, such as metallic compounds or large conjugated molecules.
• Transition metal complexes and lanthanides, particularly those with localized open-shell configurations.
• Diradicals and systems with dissociating bonds, like those found in transition state structures.

3. How does the choice of SCF algorithm affect convergence? The SCF algorithm is a critical factor. The standard DIIS (Direct Inversion in the Iterative Subspace) algorithm is aggressive and fast for well-behaved systems but can oscillate or diverge for difficult cases. For these, more robust alternatives are available [20] [10]:

• MESA, LISTi, EDIIS: Often more stable convergence accelerators than DIIS for specific problem classes [20].
• Second-Order Convergers (TRAH, NRSCF, AHSCF): These methods use energy second derivatives and are much more robust but also more computationally expensive per iteration. Some programs, like ORCA, can automatically switch to a second-order method like TRAH (Trust Radius Augmented Hessian) if DIIS struggles [10].

4. When should I consider adjusting the integration grid in DFT calculations? A numerical integration grid that is too coarse can introduce noise into the Fock matrix construction, leading to convergence oscillations, especially in the first few iterations [10]. If you observe oscillatory behavior, increasing the grid size (e.g., from Grid4 to Grid5 in ORCA) is a recommended step. This issue is less common with modern code and default grids but should not be overlooked [10].

5. What is the role of electron smearing and level shifting? These techniques can force convergence but slightly alter the physical problem.

• Electron Smearing: Assigns fractional occupation numbers to orbitals near the Fermi level, which is particularly helpful for metallic systems or those with many near-degenerate states. The smearing value should be kept as low as possible to minimize its impact on the total energy [20].
• Level Shifting: Artificially raises the energy of unoccupied (virtual) orbitals. While effective, it can give incorrect values for properties that involve virtual orbitals, such as excitation energies or NMR chemical shifts [20].

6. My geometry optimization fails because the SCF won't converge at a specific step. What can I do? The default behavior in many quantum chemistry codes (e.g., ORCA) is to continue an optimization if the SCF is "nearly converged" but to stop entirely if it is far from convergence [10]. To resolve this:

• Use a converged wavefunction from a previous, successfully optimized geometry as the initial guess for the new step.
• For the problematic geometry, run a single-point energy calculation first, using the advanced convergence techniques listed below to obtain a converged density.
• Once a stable wavefunction is found for that geometry, you can restart the optimization.

---

Advanced SCF Convergence Protocols

For systems that resist initial troubleshooting, a more methodical approach is required. The following workflow provides a structured path to achieve convergence.

Troubleshooting Workflow for Stubborn SCF Cases

The diagram below outlines a logical escalation path for resolving persistent SCF convergence issues.

Protocol 1: Tuning DIIS Parameters for Stability

For difficult cases, the default DIIS settings can be too aggressive. Slower, more stable iterations are often more successful [20].

Methodology: Modify the %scf block (or equivalent in your code) to use more conservative parameters. The following table provides a starting point for a slow-but-steady DIIS approach [20] [10].

Table: DIIS Parameter Adjustments for Problematic Systems

Parameter	Standard Default	Recommended for Difficult Cases	Function
DIISMaxEq (N)	5-10 [20] [10]	15-40 [10]	Number of previous Fock matrices used for extrapolation. More vectors increase stability.
Mixing	0.1-0.3 [20]	0.015-0.05 [20]	Fraction of new Fock matrix used. Lower values dampen oscillations.
Cyc	5 [20]	20-30 [20]	Number of initial SD iterations before DIIS starts.
MaxIter	100-125 [10]	500-1500 [10]	Maximum number of SCF cycles.

Example Input (ORCA-style):

Protocol 2: Employing Second-Order Convergence Methods

When first-order methods (like DIIS) fail, second-order methods that use the Hessian (energy second derivative) can often succeed.

Methodology: Activate a second-order algorithm. In ORCA, this is often the TRAH algorithm, which may activate automatically [10]. You can also force the use of other algorithms like KDIIS combined with the SOSCF (Supervised Orbital Optimization SCF). For open-shell systems, SOSCF may need to be manually enabled and its start threshold tightened [10].

Example Input (ORCA):

Protocol 3: Strategies for Pathological Systems (e.g., Metal Clusters)

For truly challenging systems like iron-sulfur clusters, a combination of maximum stabilization techniques is required [10].

Methodology: This protocol uses maximum damping, frequent recalculation of the Fock matrix to eliminate numerical noise, and a large number of iterations.

Example Input (ORCA):

---

The Scientist's Toolkit: Research Reagent Solutions

Table: Essential Computational Parameters and Their Functions

Tool/Parameter	Primary Function	Application Context
Integration Grid	Defines points for numerical integration in DFT.	Coarse grids can cause oscillation; refine to aid convergence [10].
Auxiliary Basis Set	Expands electron density in RI-J and related methods.	Must be matched to the orbital basis set for accuracy and stability.
DIIS Accelerator	Extrapolates Fock matrices from previous cycles.	The standard, aggressive converger. Tune parameters (see Table 2) for stability [20] [10].
TRAH / NRSCF	Second-order SCF convergence algorithms.	Robust fallback for systems where DIIS fails [10].
Electron Smearing	Occupies orbitals near Fermi level with fractional electrons.	Essential for metallic systems and small-gap semiconductors [20].
Level Shifting	Artificially raises energy of virtual orbitals.	Forces convergence but invalidates properties using virtual orbitals [20].
Damping	Mixes a large fraction of the old density with the new.	Suppresses oscillations in the initial SCF cycles [10].
Ghost Atoms (BSSE)	Estimates basis set superposition error via the Counterpoise method.	Critical for accurate computation of weak interaction energies [47].
5-Phenethylisoxazol-4-amine	5-Phenethylisoxazol-4-amine|Research Chemical	5-Phenethylisoxazol-4-amine is a chemical reagent for research use only (RUO). Explore its potential applications in medicinal chemistry and pharmacology. Not for human consumption.

---

Key Quantitative Data for SCF Control

The table below summarizes critical quantitative parameters from the troubleshooting guides, providing a quick reference for configuring your calculations.

Table: Key SCF Control Parameters and Their Effects

Parameter	Default Value	Stability-Oriented Value	Effect of Adjustment
SCF Max Iterations	125 [10]	400-1500 [10] [35]	Allows more time to reach convergence.
DIIS Memory (N)	5-10 [20] [10]	25 [20]	Increases stability but uses more memory.
Initial Damping (Mixing1)	0.2 [20]	0.09 [20]	Slows down the initial SCF cycles for stability.
Mixing Parameter	0.1-0.3 [20]	0.015 [20]	Reduces step size, preventing oscillation.
SOSCF Start Threshold	0.0033 [10]	0.00033 [10]	Engages the more powerful SOSCF algorithm earlier.
DIIS Start Cycle (Cyc)	5 [20]	30 [20]	More initial equilibration cycles before acceleration.

FAQs and Troubleshooting Guides

FAQ 1: My geometry optimization oscillates without converging, even though my system has a low HOMO-LUMO gap. What advanced techniques can I use? When the HOMO-LUMO gap is small, electronic structure changes between optimization steps can prevent convergence. Fractional Occupations and Energy Shifting are two key techniques to address this.

• Fractional Occupations: This method smears the electron density around the Fermi level by allowing fractional occupation numbers for orbitals near the HOMO-LUMO gap. This stabilizes the SCF procedure against small changes in the geometry that would otherwise cause large, discontinuous changes in the total energy. It is implemented using an OCCUPATIONS block to freeze the number of electrons per symmetry.
• Energy Shifting: This technique artificially shifts the orbital energies of the virtual (unoccupied) orbitals. By applying a shift, it effectively increases the HOMO-LUMO gap in the Hamiltonian, which improves the conditioning of the SCF equations and leads to more stable convergence during the optimization cycle.

FAQ 2: After applying fractional occupations, my optimization converges but the bond lengths are unrealistically short. What is the cause? Excessively short bond lengths often indicate a basis set problem, particularly when using the Pauli relativistic method [7].

• Primary Cause: The issue can be the onset of a "Pauli variational collapse," especially if small or absent frozen cores are used with large basis sets on heavy elements. Alternatively, using large frozen cores can cause them to overlap at short bond distances, missing repulsive terms and leading to a spurious "core collapse" [7].
• Recommended Cure: The most robust solution is to abandon the Pauli method and use the ZORA relativistic approach instead. If you must use the Pauli formalism, consider using bigger frozen cores or reducing the flexibility of the basis set's s- and p-functions [7].

FAQ 3: What general steps should I take if my geometry optimization fails to converge? First, analyze the behavior of the energy over the last ten iterations [7].

• Consistent Energy Change: If the energy is consistently decreasing (or increasing) with occasional jumps, the optimization is likely proceeding correctly but needs more time. Simply increase the number of iterations and restart from the latest geometry [7].
• Energy Oscillation: If the energy oscillates around a value and the gradient stops improving, the problem likely lies in the calculation setup. In such cases, systematically increasing the numerical accuracy is crucial [7].

Detailed Experimental Protocols

Protocol 1: Implementing an Advanced SCF Convergence Procedure

This protocol outlines the steps to tighten key accuracy settings to achieve stable SCF convergence for difficult systems [7].

Step	Parameter	Action	Rationale
1	Numerical Quality	Increase from Normal to Good.	Uses a more extensive integration scheme and larger basis set for more accurate force calculations [7].
2	SCF Convergence	Tighten to 1e-8 or 1e-9.	Reduces numerical noise in the energy and gradients, providing a cleaner signal to the geometry optimizer [7].
3	Density	Select Exact in the XC-potential (use ExactDensity keyword).	Uses the exact computed density instead of a fitted model, improving accuracy at the cost of speed [7].
4	Basis Set	Use a high-quality basis like TZ2P.	Provides better flexibility for describing subtle changes in electron density during bond formation and breaking [7].

Protocol 2: Applying Fractional Occupations for Metallic Systems

This methodology is used to stabilize the SCF procedure in systems with a very small or zero HOMO-LUMO gap.

Step	Procedure	Specification
1	Identify Degenerate Orbitals	After an initial SCF calculation, analyze the orbital eigenvalues to identify orbitals near the Fermi level that are prone to crossing.
2	Define Symmetry Block	Determine the irreducible representation (symmetry label) of the problematic orbitals.
3	Construct OCCUPATIONS Block	In the input, specify the number of electrons to be held fixed for that symmetry block. For example, to assign 0.5 electrons to each of four degenerate orbitals, you would fix the total occupancy for that block to 2.0 electrons.
4	Restart Optimization	Run the geometry optimization using the modified occupation scheme.

The Scientist's Toolkit: Research Reagent Solutions

The following table details key computational "reagents" and their functions in advanced geometry optimization.

Research Reagent	Function & Explanation
TZ2P Basis Set	A triple-zeta basis set with two polarization functions. It provides a high-quality description of valence electron behavior and is essential for accurate gradient calculations [7].
Exact Density (ExactDensity)	A keyword that instructs the code to use the exact, unfitted electron density when constructing the Kohn-Sham potential. This avoids numerical errors from density fitting, crucial for sensitive systems [7].
ZORA Relativistic Method	The Zeroth-Order Regular Approximation is a scalar relativistic method. It is preferred over the Pauli method to avoid basis set collapse and provide accurate results for systems containing heavy elements [7].
OCCUPATIONS Block	An input block that allows manual control over electron occupancy per symmetry. This is the primary method for implementing fractional occupations to stabilize calculations with small HOMO-LUMO gaps [7].
Delocalized Coordinates	The internal coordinate system used by the geometry optimizer. Using delocalized coordinates instead of Cartesian coordinates typically leads to faster convergence and is more robust for complex molecular systems [7].

Workflow Visualization

The following diagram illustrates the logical decision process for applying these advanced techniques within an automated SCF convergence and geometry optimization framework.

Overcoming Challenges in Metallic Systems and Complex Biomolecules

Troubleshooting Guides

SCF Convergence Failure

Q: My self-consistent field (SCF) calculation oscillates or fails to converge. What steps can I take?

A: SCF convergence problems are common in systems with metallic character, small HOMO-LUMO gaps, or complex electronic structures. Implement the following methodological improvements:

• Increase Computational Accuracy: Tighten key parameters to improve the quality of your initial results.
  • Set NumericalQuality to Good.
  • Tighten the SCF convergence criterion (e.g., Converge 1e-7 or 1e-8).
  • For the highest accuracy in the XC-potential, use the ExactDensity keyword, noting this will significantly increase computation time [7].
• Adjust SCF Acceleration Algorithm: The default DIIS or ADIIS+SDIIS methods may not be optimal for all systems [34].
  • For problematic cases: Switch to the MultiSecant method, which is robust and comes at no extra cost per cycle [6].
  • Alternative methods: Consider LISTi or other LIST family methods, which can be selected using the AccelerationMethod key [34].
  • Conservative mixing: Reduce the SCF mixing parameter (e.g., Mixing 0.05) and/or the DIIS%Dimix parameter (e.g., 0.1) for more stable convergence [6].
• Employ Finite Electronic Temperature: For geometry optimizations where the initial geometry is far from converged, using a finite electronic temperature can aid SCF convergence. This can be automated to start with a higher temperature and tighten as the geometry converges [6].
• Check for Fundamental Issues: A small HOMO-LUMO gap can lead to changing electronic structures between steps. Verify you have the correct ground state and consider freezing electron occupations per symmetry if oscillations are between orbitals of different symmetry [7].

Table: Key SCF Input Parameters for Troubleshooting

Parameter	Default/Typical Value	Troubleshooting Value	Function
SCF Converge	1e-6	1e-7 or 1e-8	Tightens the energy convergence criterion [7]
SCF Mixing	0.2	0.05	Reduces the amount of new density mixed in per cycle for stability [6] [34]
NumericalQuality	Normal	Good	Improves the quality of numerical integration [7]
AccelerationMethod	ADIIS	MultiSecant or LISTi	Changes the algorithm used to accelerate SCF convergence [6] [34]

Geometry Optimization Not Converging

Q: The molecular geometry optimization is oscillating or will not converge to a minimum. How can I fix this?

A: Geometry optimization failures can stem from inaccurate forces or an unstable optimization pathway.

• Improve Gradient Accuracy: Inaccurate forces (gradients) derail optimizations.
  • Increase the NumericalQuality to Good [7] [6].
  • For methods using numerical grids (like ADF), increase the number of radial points (e.g., RadialDefaults NR 10000) [6].
  • Use ExactDensity and a tighter SCF convergence for the most accurate gradients [7].
• Switch to Delocalized Internal Coordinates: Optimization in Cartesian coordinates often requires more steps than in delocalized internal coordinates. If you haven't tried delocalized coordinates, you should do so [7].
• Address Specific Geometric Instabilities:
  • Near-180-degree angles: If a bond angle becomes close to 180 degrees during optimization, it can cause instability. Restarting the optimization from the latest geometry can help. As a last resort, constrain the angle to a value close to, but not equal to, 180 degrees [7].
  • Constraints and Symmetry: Be aware that applying constraints can break the inherent symmetry of the system, which may lead to convergence issues [7].
• Leverage Neural Network Potentials (NNPs): For large systems like biomolecules, using a pre-trained NNP like Meta's Universal Model for Atoms (UMA) or eSEN can provide much faster and better-behaved geometry optimizations. These models, trained on massive datasets like OMol25, can offer "DFT-level accuracy" at a fraction of the cost, avoiding many traditional SCF and optimization problems [48].

Unrealistically Short Bond Lengths in Metals

Q: My optimized metal-ligand bonds are significantly shorter than expected. What is the cause?

A: This is a known issue, often related to the basis set and relativistic treatment.

• Avoid the Pauli Relativistic Method: The primary cause for overly short bonds, especially with heavy elements, is often the onset of "Pauli variational collapse." The best solution is to avoid the Pauli formalism and use the ZORA relativistic approach instead [7].
• Check Frozen Core Approximations:
  • Problem: If frozen cores are too small or absent when using the Pauli method, it can lead to variational collapse [7].
  • Problem: If frozen cores are too large, they may start to overlap at short bond lengths, missing repulsive terms and leading to a spurious "core collapse" and short bonds [7].
  • Action: Carefully evaluate your frozen core settings relative to your bond lengths.

Table: Troubleshooting Short Bonds in Metallic Systems

Symptom	Possible Cause	Recommended Cure
Bonds are too short; using Pauli method	Basis set trouble / onset of Pauli variational collapse	Abandon the Pauli method; use ZORA instead [7]
Bonds are too short; large frozen cores	Frozen cores overlapping, missing repulsion	Use smaller frozen cores (but be wary of using Pauli) [7]
Bonds are too short; Pauli method required	Variational collapse with small frozen cores	Use larger frozen cores and/or reduce basis set flexibility [7]

Experimental Protocols for High-Accuracy Modeling

Protocol 1: High-Accuracy Single-Point Energy & Gradient Calculation

This protocol is designed to generate benchmark-quality data for training machine learning potentials or for final energy evaluations on pre-optimized geometries.

• Method and Basis Set:
  • Functional: ωB97M-V, a state-of-the-art range-separated meta-GGA functional that avoids many pathologies of older functionals [48] [49].
  • Basis Set: def2-TZVPD [48] [49].
• Accuracy Settings:
  • NumericalQuality Good
  • SCF Converge 1e-8
  • Use a large pruned (99,590) integration grid for accurate non-covalent interactions and gradients [48].
• Relativistic Treatment:
  • For elements heavier than Kr, use the ZORA Hamiltonian to avoid known issues with bond shortening from the Pauli method [7].

Protocol 2: Robust Geometry Optimization for Challenging Systems

This workflow uses a multi-stage approach to efficiently and reliably locate minima, especially for systems prone to SCF or geometric convergence issues.

Diagram: Robust Multi-Stage Optimization Workflow

The Scientist's Toolkit: Research Reagents & Computational Solutions

Table: Essential Resources for Modern Computational Chemistry

Item Name	Type	Function / Application
OMol25 Dataset [48] [49]	Dataset	A massive dataset of >100 million molecular calculations at ωB97M-V/def2-TZVPD level. Used for training and benchmarking ML models for diverse chemistry, including biomolecules and metal complexes.
Universal Model for Atoms (UMA) [48]	Neural Network Potential (NNP)	A pre-trained model that provides DFT-level accuracy at a fraction of the cost. Ideal for rapid geometry optimizations and MD simulations on large systems (e.g., proteins, electrolytes).
eSEN Model (conserving-force) [48]	Neural Network Potential (NNP)	An architecture providing smooth potential energy surfaces. The conserving-force variant is recommended for reliable molecular dynamics and geometry optimization.
Projector Augmented Wave (PAW) [50]	Pseudopotential Method	A highly accurate pseudopotential method used in plane-wave DFT to model core electrons, balancing computational cost and accuracy. Can be optimized for specific elements.
GFN2-xTB [48]	Semiempirical Method	A fast, low-cost quantum chemical method useful for generating initial geometries, sampling conformers, or pre-screening in high-throughput workflows.
libxc [5]	Software Library	A library providing a vast collection of exchange-correlation functionals for DFT, enabling functional development and standardized testing.
CREST [5]	Software	The state-of-the-art tool for conformer searching using metadynamics, essential for exploring the configurational space of complex biomolecules.
PCC-GCMC Framework [51]	Computational Workflow	A technique (Periodic Configuration Construction via Grand Canonical Monte Carlo) to convert non-periodic defect clusters into periodic configurations compatible with standard plane-wave DFT codes. Critical for modeling extended defects in metals.

Automated Fallback Strategies and Adaptive Parameter Tuning

Troubleshooting Guide: Resolving SCF Convergence Failures

Q: My self-consistent field (SCF) calculation will not converge. What are the first steps I should take?

A: Initial diagnostics should focus on the behavior of the SCF energy and the molecular system itself.

• Check Energy Trends: Examine the last ten or so iterations. If the energy is changing monotonically (more or less consistently decreasing or increasing), the calculation is likely progressing but slowly. Simply increasing the maximum number of SCF iterations (MAX_SCF_CYCLES in Q-Chem, MaxIter in ORCA) may resolve the issue [10] [7] [30].
• Check the Geometry: Ensure your starting geometry is reasonable. An unreasonable geometry can prevent convergence [10].
• Check the HOMO-LUMO Gap: A small HOMO-LUMO gap can indicate that the electronic structure is changing between optimization steps, leading to non-convergence. This may require checking if you have the correct ground state or freezing electron occupancies per symmetry [7].

Q: I have performed the initial checks, but the SCF still oscillates or fails. What advanced strategies should I employ?

A: If basic steps fail, implement a structured fallback strategy. The following workflow and table outline a systematic approach.

Table: Advanced SCF Convergence & Fallback Techniques

Method Category	Specific Action	Key Parameters / Keywords	Effect & Rationale
Improve Guess Orbitals [10] [30]	Converge a simpler calculation (e.g., BP86/def2-SVP) and read its orbitals.	! MORead in ORCA; %moinp "guess.gbw"	Provides a better starting point, steering the SCF away from problematic regions of the wavefunction space.
Tighten Numerical Accuracy [7]	Use a higher quality integration grid and tighter SCF convergence.	NumericalQuality Good, SCF converge 1e-8 in ADF; SCF_CONVERGENCE 8 in Q-Chem	Reduces numerical noise in the Fock matrix and energy gradients, leading to more stable convergence.
Algorithm Fallback [30]	Switch from the default DIIS algorithm to a more robust Geometric Direct Minimization (GDM).	SCF_ALGORITHM = DIIS_GDM or GDM in Q-Chem	GDM is highly robust and better at converging to a local minimum on challenging surfaces. The hybrid DIIS_GDM uses DIIS initially for efficiency.
Damping & Shift [10]	Apply damping to control large initial oscillations in the SCF procedure.	! SlowConv or ! VerySlowConv in ORCA	Suppresses oscillations by mixing a larger fraction of the old Fock/Density matrix into the new one, stabilizing early iterations.
Second-Order Convergers [10]	Activate a second-order convergence algorithm like TRAH.	AutoTRAH true (default in ORCA 5.0+)	A robust, albeit more expensive, method that automatically activates if the standard DIIS converger struggles.

Q: My system contains transition metals or is open-shell. Are there special considerations?

A: Yes, these systems are notoriously difficult to converge [10].

• Use Damping: Start with the ! SlowConv keyword in ORCA, which applies damping parameters suitable for such pathological cases [10].
• Adjust DIIS: For very difficult systems (e.g., metal clusters), increase the DIIS subspace size and the direct reset frequency [10].
  • DIISMaxEq 15 (increases stored Fock matrices for extrapolation)
  • directresetfreq 1 (rebuilds the full Fock matrix every iteration to eliminate numerical noise)
• Try KDIIS: The KDIIS algorithm, sometimes combined with SOSCF, can offer faster convergence for some transition metal complexes [10].

---

FAQs on Adaptive Parameter Tuning

Q: What is the core idea behind adaptive parameter tuning in this context?

A: It refers to strategies that predefine how key computational parameters are modified during a calculation based on its progress, rather than keeping them fixed. This allows for dynamic balancing of exploration (e.g., finding the correct electronic state) and exploitation (precise convergence) [52]. In adaptive learning frameworks, this process can be automated, using performance metrics to guide the tuning [53].

Q: Can you provide a concrete example of an adaptive parameter schedule?

A: A common application is adapting the learning rate in machine learning, a concept that can be analogously applied to parameters in computational chemistry. The following table summarizes three classic adapter functions [52].

Table: Common Parameter Adapter Functions

Adapter Type	Mathematical Form	Key Parameter (α)	Behavior
Exponential	( V(t) = end_value + (initial_value - end_value) * e^{-α * t} )	α > 0	Rapid initial decay that slows over time. Larger α means faster decay.
Inverse	( V(t) = end_value + (initial_value - end_value) / (1 + α * t) )	α > 0	smoother, more gradual decay compared to the exponential adapter.
Potential	( V(t) = end_value + (initial_value - end_value) / (1 + α * t)^β )	0 < α < 1	The most rapidly decaying function among the three for a fixed α.

Q: How can more advanced AI techniques be used for adaptive tuning?

A: Reinforcement Learning (RL) can automate the design and optimization of computational models. For instance, a framework can use RL to search for the optimal architecture of a Graph Neural Network by dynamically exploring a defined search space and optimizing based on performance metrics, creating a model tailored to a specific dataset or task without manual intervention [53].

---

Experimental Protocols for Automated Fallback & Tuning Research

Protocol 1: Benchmarking SCF Fallback Strategies

• System Selection: Curate a test set of molecular systems with known convergence difficulties (e.g., open-shell transition metal complexes, conjugated radical anions) [10].
• Baseline Calculation: Attempt to converge each system using a standard method (e.g., SCF_ALGORITHM=DIIS in Q-Chem) with default settings [30].
• Intervention Trigger: Define a trigger for fallback, such as the DIIS error being above a threshold (THRESH_DIIS_SWITCH) after a set number of cycles (MAX_DIIS_CYCLES) [30].
• Fallback Activation: Upon triggering, switch to a robust algorithm like Geometric Direct Minimization (GDM) [30].
• Metric Collection: For each system and strategy, record: a) Success (Yes/No), b) Total SCF Iterations, c) Final SCF Energy, and d) Total Wall Time.

Protocol 2: Evaluating Adaptive Learning for Model Design This protocol is based on the Adaptive-DTA framework for drug-target affinity prediction, which exemplifies automated model tuning [53].

• Define Search Space: Specify a flexible search space of possible model architectures using a Directed Acyclic Graph (DAG), containing various neural network layer types and connection options.
• Implement Search Strategy: Employ a Reinforcement Learning (RL) agent to explore the search space. The agent's goal is to discover a high-performing model architecture.
• Two-Stage Validation:
  • Low-Fidelity (LF) Stage: Quickly evaluate a large number of candidate architectures using a smaller subset of data or fewer training epochs.
  • High-Fidelity (HF) Stage: Take the top-performing candidates from the LF stage and evaluate them thoroughly on the full validation set.
• Performance Comparison: Benchmark the best automatically discovered model against state-of-the-art, hand-designed models on established benchmark datasets (e.g., Davis, KIBA for drug-target affinity).

---

The Scientist's Toolkit: Research Reagent Solutions

Table: Essential Computational Tools for SCF & Optimization Research

Tool / "Reagent"	Function	Example Use Case
DIIS (Direct Inversion in Iterative Subspace) [30]	An extrapolation algorithm that accelerates SCF convergence by using information from previous iterations to generate an improved guess for the next Fock matrix.	Default algorithm in many quantum chemistry codes for rapid convergence of well-behaved systems.
GDM (Geometric Direct Minimization) [30]	A robust algorithm that minimizes the SCF energy directly, properly accounting for the curved geometry of orbital rotation space.	Primary fallback algorithm when DIIS fails or for restricted open-shell calculations.
TRAH (Trust Region Augmented Hessian) [10]	A second-order SCF convergence method that is very robust but computationally more expensive.	Automatically activated in ORCA for difficult cases; excellent for pathological systems.
SOSCF (Second-Order SCF) [10]	A method that uses an approximate Hessian to take more sophisticated steps toward convergence.	Can be used to speed up convergence once a threshold (e.g., orbital gradient) is reached.
Two-Stage Training [53]	A validation strategy that uses fast, low-fidelity screening of many options followed by rigorous, high-fidelity validation of the best candidates.	Core component of the Adaptive-DTA framework for efficiently searching a vast model architecture space.

Frequently Asked Questions

Why is simply increasing the maximum number of SCF cycles an ineffective solution? Increasing the cycle limit (e.g., MaxCycle in Gaussian, MaxIter in ORCA) does not address the root cause of the non-convergence. If the Self-Consistent Field (SCF) procedure is oscillating wildly or has stalled, more iterations will not help it find a solution. It merely prolongs the computation time without guaranteeing convergence, effectively wasting computational resources [4] [10].

What does the scientific community say about this approach? Experts explicitly advise against it. One technical blog notes that this method is "normally useless," explaining that if the SCF energy is oscillating, increasing the number of steps is meaningless [4]. Similarly, the ORCA input library suggests that this is only a viable tactic if the calculation is almost converged and just needs a few more steps; otherwise, it is pointless [10].

What are the risks of forcing a calculation to continue after non-convergence? Using keywords like IOp(5/13=1) in Gaussian to ignore convergence failure and continue the job is considered a "stupid method" and should never be used [4]. Performing geometry optimization or frequency analysis on a non-converged wavefunction can lead to inaccurate geometries, energies, and property predictions, compromising the entire research outcome.

Troubleshooting Guide: Effective Strategies for SCF Convergence

Instead of increasing cycle limits, follow this systematic troubleshooting workflow to address the underlying problem.

Diagram: A systematic workflow for resolving SCF convergence issues.

Step 1: Check the Molecular Geometry and Basis Set

A problematic geometry or an overly large basis set can be the root cause.

• Protocol: Visually inspect the molecular structure for unreasonable bond lengths or angles. For a difficult case, try a smaller or less diffuse basis set to obtain an initial converged wavefunction [4].
• Solution: Once converged with a smaller basis, use the guess=read keyword to use these orbitals as the initial guess for a second calculation with your target, larger basis set [4] [10].

Step 2: Modify the SCF Algorithm

The default DIIS algorithm can sometimes hinder convergence.

• Protocol: Switch to a more robust algorithm. The Quadratic Convergence (QC) method is often helpful for difficult cases, though it is slower [4] [28]. In ORCA, the Trust Radius Augmented Hessian (TRAH) algorithm activates automatically if the standard method struggles and is a robust second-order converger [10].
• Solution: Use the SCF=QC keyword in Gaussian. In ORCA, TRAH is typically automatic, but you can disable it with ! NoTrah if it performs poorly [28] [10].

Step 3: Improve the Initial Wavefunction Guess

A poor initial guess can lead the SCF procedure down a path with no convergence.

• Protocol: Calculate a simpler, more stable system. This could be a closed-shell cation of your open-shell system, or a calculation using a different, more stable functional (e.g., BP86) [4] [10].
• Solution: Use the guess=read keyword (Gaussian) or ! MORead (ORCA) to read the converged orbitals from the simpler calculation into the problematic one [4] [10].

Step 4: Apply Convergence Aids

These techniques help stabilize the SCF iterative process.

• Protocol 1 - Level Shifting: Artificially increases the energy of the virtual orbitals, reducing mixing with occupied orbitals. This is especially useful for systems with a small HOMO-LUMO gap, such as those containing transition metals [4] [10].
• Solution: In Gaussian, use SCF=vshift=500. In ORCA, use the Shift keyword in the %scf block [4] [10].
• Protocol 2 - Fermi Broadening & Damping: Introduces electronic smearing to avoid oscillations between two similar energy states in the early stages of the SCF [28] [10].
• Solution: Use the SCF=Fermi keyword in Gaussian. In ORCA, the ! SlowConv keyword applies damping which can be beneficial for transition metal complexes [28] [10].

Comparison of Ineffective vs. Effective Methods

The table below summarizes why increasing cycles fails and what to do instead.

Method	Key Implementation	Rationale for Ineffectiveness	Recommended Alternative
Increase Cycle Limit	SCF=MaxCycle=128 (Gaussian)	Fails to address the core issue (e.g., bad guess, oscillations).	Systematically troubleshoot using the guide above.
Ignore Convergence	IOp(5/13=1) (Gaussian)	Forces calculation to continue, producing physically meaningless results.	Use SCF=QC or SCF=XQC for a robust algorithm [4] [28].
Default Settings Only	N/A	Default algorithms (e.g., DIIS) are not optimal for all systems.	For transition metals, use ! SlowConv and SOSCF in ORCA [10].

The Scientist's Toolkit: Key Research Reagent Solutions

This table lists essential "reagents" or keywords for handling SCF convergence in computational chemistry.

Item / Keyword	Function	Application Context
SCF=QC	Enables a quadratically convergent algorithm [28].	Difficult cases in Gaussian; not for Restricted Open-Shell (ROHF).
Guess=Read	Reads the wavefunction from a previous calculation [4].	Providing a good initial guess from a stable system.
SCF=VShift	Applies an energy level shift to virtual orbitals [4] [28].	Systems with small HOMO-LUMO gaps (e.g., transition metals).
! SlowConv	Applies stronger damping during SCF iterations [10].	Open-shell transition metal complexes in ORCA.
! MORead	Reads initial molecular orbitals from a file [10].	ORCA equivalent of guess=read.
SCF=NoVarAcc	Prevents grid reduction at the start of a calculation [4].	Calculations using diffuse functions in Gaussian.
SCF=Conver=6	Relaxes the SCF convergence criterion by 100x [4].	Use with caution. Only for single-point calculations where high precision is not critical.

Benchmarking and Validation Frameworks for Automated SCF Protocols

Frequently Asked Questions (FAQs)

1. What does the "SCF not converged" error mean, and why is it a problem? The Self-Consistent Field (SCF) procedure is an iterative method to solve the electronic structure of a system. An "SCF not converged" error indicates that this iterative process failed to find a stable, consistent solution within the set number of cycles. This is problematic because all subsequent results—including single-point energies, optimized geometries, and molecular properties—are unreliable and should not be used [10].

2. What are the main physical reasons an SCF calculation might fail to converge? Several physical and numerical factors can cause convergence failure:

• Small HOMO-LUMO Gap: Systems with a very small energy difference between the highest occupied and lowest unoccupied molecular orbitals are prone to oscillation in orbital occupation or "charge sloshing," where the electron density fluctuates wildly between iterations [2].
• Poor Initial Guess: The starting point for the electron density may be too far from the final solution, particularly for systems with unusual electronic structures, such as open-shell transition metal complexes or molecules with multi-reference character [10] [2].
• Unrealistic Molecular Geometry: A starting geometry that is chemically unreasonable, such as atoms being too close together or bonds being overly stretched, can make it impossible to find a stable electronic solution [10] [2].
• Numerical Instabilities: The use of diffuse basis sets or integration grids of insufficient quality can introduce numerical noise that prevents convergence [10] [2] [4].

3. My geometry optimization stopped due to an SCF failure in one cycle. What should I do? The default behavior in many quantum chemistry packages like ORCA is to stop a geometry optimization only if the SCF fails completely. If it is "nearly converged," the optimization may continue, as the problem often resolves in later steps. However, if it stops completely, you should:

• Check the geometry from the last successful step for reasonableness.
• Modify your SCF settings to be more robust (see troubleshooting guide below) and restart the optimization [10].

4. Is increasing the maximum number of SCF cycles (MaxIter) a reliable solution? Increasing MaxIter is only helpful if the SCF energy is showing a clear, steady trend toward convergence. If the energy is oscillating, simply increasing the cycle limit is ineffective and a different convergence algorithm or damping strategy is needed [10] [4].

5. When is it acceptable to use a looser SCF convergence criterion? Loosening the convergence criterion (e.g., from TightSCF to normal) can be acceptable for single-point energy calculations where high precision is not critical, as the energy often converges well before the density matrix. However, it is not recommended for geometry optimizations or frequency calculations, as it can lead to inaccurate forces and hinder the optimization process itself [4].

Troubleshooting Guide: Resolving SCF Convergence Failures

Follow this systematic workflow to diagnose and fix SCF convergence problems.

Step 1: Diagnose the Problem

Examine your SCF output log to identify the convergence behavior.

Observation	Likely Cause & Relevant Metrics
Steady but slow convergence; energy delta (DeltaE) decreasing too slowly.	Poor initial guess or system inherently slow to converge. Monitor DeltaE and orbital gradients (MaxP, RMSP) [10].
Wild oscillations in energy (large amplitude).	Small HOMO-LUMO gap leading to "charge sloshing" or occupation flipping [2].
Small, noisy oscillations in energy (tiny amplitude).	Numerical instabilities from a poor-quality integration grid or a nearly linear-dependent basis set [2] [4].

Step 2: Apply Simple, Universal Fixes

These methods are fast and work for many common issues.

• Improve the Initial Guess: Instead of the default, try alternative initial guesses like Guess=Huckel or Guess=INO [4]. For difficult systems, a reliable strategy is to converge the SCF with a smaller basis set (e.g., def2-SVP) and then use the resulting orbitals as the guess for a larger basis set calculation with Guess=Read [10] [6] [4].
• Converge a Simpler System: Try to converge the SCF for a closed-shell ion (cation or anion) of your system. The resulting orbitals can often be used as an excellent starting guess for the target open-shell or neutral system [10] [4].
• Increase Integration Grid Quality: For DFT calculations, especially with meta-GGA or hybrid functionals, increasing the integration grid size (e.g., to Int=UltraFine in Gaussian) can remove numerical noise that hinders convergence [4].

Step 3: Apply Advanced Fixes for Specific Symptoms

• For Oscillations/Small HOMO-LUMO Gap:

  • Damping: Use keywords like SlowConv or VerySlowConv to dampen the updates to the density matrix between cycles [10].
  • Level Shifting: Apply a small energy shift (e.g., 300-500 cm⁻¹) to the virtual orbitals to artificially increase the HOMO-LUMO gap. This stabilizes the SCF process and does not affect the final converged result [10] [4].
  • DIIS Management: In rare cases, the default DIIS algorithm can cause divergence. Turning it off with SCF=NoDIIS can help, though convergence will be slower [4].

• For Slow but Steady Convergence:

  • Use a Second-Order Converger: Enable a second-order convergence algorithm (e.g., SOSCF, NRSCF, or AHSCF). In ORCA, the Trust Radius Augmented Hessian (TRAH) method is designed to handle difficult cases and may activate automatically [10].
  • Try KDIIS: The KDIIS algorithm can sometimes lead to faster convergence than standard DIIS [10].

Step 4: Last Resorts for Pathological Cases

For extremely difficult systems like metal clusters, more expensive settings may be required.

• Increase DIIS Space: Increase the number of previous Fock matrices used in the DIIS extrapolation (e.g., DIISMaxEq 15-40) [10].
• Full Fock Matrix Rebuild: Set directresetfreq 1 to rebuild the Fock matrix from scratch in every iteration, eliminating accumulation of numerical errors. This is computationally expensive but can be necessary [10].

The Scientist's Toolkit: Research Reagent Solutions

The following table details key computational "reagents" and their functions in troubleshooting SCF convergence.

Research Reagent / Keyword	Function & Application
SlowConv / VerySlowConv	Applies damping to stabilize the SCF procedure during initial iterations, crucial for oscillating systems and transition metal complexes [10].
SOSCF (Second-Order SCF)	Accelerates convergence once a threshold is reached by using more expensive but more efficient second-order methods [10].
Level Shift (VShift)	Artificially increases the HOMO-LUMO gap during the SCF process to prevent occupation flipping and charge sloshing, without impacting final energy [10] [4].
Guess=Read	Instructs the program to use orbitals from a previously converged calculation as the initial guess, often the most effective way to start a difficult calculation [10] [4].
Integration Grid (Int)	Defines the numerical grid for integrating exchange-correlation functionals in DFT. A finer grid (UltraFine) improves accuracy and can aid convergence [4].

Experimental Protocols for Robust SCF in Automated Workflows

For research focused on automated geometry optimization, integrating robust SCF protocols is essential. The following workflow diagram and protocol outline a hierarchical strategy.

Protocol: A Hierarchical SCF Strategy for Geometry Optimization

• Initialization:

  • Generate a reasonable molecular geometry.
  • For systems suspected to be difficult (e.g., containing transition metals), begin directly at Level 2.

• Level 1 (Default):

  • Use the program's default SCF settings with a standard integration grid.
  • Metrics for Success: SCF converges within the default cycle count (typically ~100-150). The final energy and density matrix stability criteria are met.

• Level 2 (Robust):

  • If Level 1 fails, activate damping (SlowConv) and a second-order converger (SOSCF or rely on automatic TRAH activation in ORCA).
  • Metrics for Success: SCF converges with damping. Monitor orbital gradients for steady decrease.

• Level 3 (Fallback):

  • If Level 2 fails or is too slow, switch to the KDIIS algorithm, increase the maximum number of iterations (MaxIter 500), and slightly relax the convergence criterion (SCF=Conver=6) for the optimization cycles only.
  • Metrics for Success: SCF converges with a larger number of cycles. The geometry optimization step completes successfully.

• Level 4 (Safe Single-Point):

  • As a last resort for a single problematic optimization step, perform a single-point calculation on the current geometry using a strong level shift (VShift=400). Once converged, read these stabilized orbitals back as the guess for the optimization step without the level shift.
  • Metrics for Success: The single-point calculation converges. The subsequent optimization step proceeds without re-triggering the SCF failure.

Validation Metric Table for Automated Workflows

Metric	Target Value	Purpose in Validation
DeltaE (Energy Change)	< 10⁻⁶ a.u. (Default)	Ensures the total energy is stationary, indicating a self-consistent solution [10].
RMSP / MaxP (Density Matrix Change)	< 10⁻⁵ / 10⁻⁴ a.u. (TightSCF)	Ensures the electron density is stable, crucial for accurate property and gradient calculations [10].
Orbital Gradient Norm	< 10⁻³ a.u.	A direct measure of how close the solution is to the true energy minimum [10].
Final Energy Deviation (with looser criteria)	< 1 kJ/mol vs. tight criteria	Validates that using a slightly looser Conver=6 for speed still yields energetically meaningful results for geometry optimization [4].

Comparative Analysis of SCF Algorithms Across Diverse Molecular Systems

Troubleshooting Guides

SCF Convergence Failure in Metal-Organic Complexes

Problem Description The self-consistent field (SCF) procedure fails to converge during geometry optimization of transition metal complexes, particularly those with open-shell configurations or near-degenerate states.

Diagnostic Steps

• Monitor Oscillation Patterns: Examine the latest 10-15 iterations. If energy changes consistently in one direction, this may indicate the starting geometry was far from minimum. If energy oscillates around a fixed value with minimal gradient changes, investigate calculation setup issues [7].
• Check HOMO-LUMO Gap: Compare the HOMO-LUMO gap at the final SCF cycle to changes in molecular orbital energies between geometries. Non-convergence may occur when these values are comparable, indicating electronic structure changes between optimization steps [7].
• Verify Spin-Polarization: Confirm the correctness of spin-polarization values in single-point calculations. Calculate high-spin states to compare energies if possible [7].

Resolution Protocols

• Increase SCF Accuracy: Tighten SCF convergence criteria to 1e-8 and increase numerical quality to "good" [7].
• Handle Near-Degeneracy: For MO repopulation between orbitals of different symmetry, freeze the number of electrons per symmetry using OCCUPATIONS blocks [7].
• Functional Selection: For transition metals, hybrid functionals like B3LYP, PBE0, or TPSSh often provide better error compensation for spin-state energetics compared to pure functionals [54].

Unphysical Bond Shortening in Heavy Element Systems

Problem Description Optimized bond lengths appear significantly too short, particularly in systems containing heavy elements where relativistic effects become important.

Diagnostic Steps

• Identify Relativistic Method: Determine if Pauli relativistic method is applied, which can cause variational collapse with inadequate frozen cores or large basis sets [7].
• Check Frozen Core Overlap: Assess whether frozen cores of neighboring atoms overlap significantly at the computed bond lengths, which can missing repulsive terms and cause "core collapse" [7].

Resolution Protocols

• Switch Relativistic Treatment: Abandon Pauli method in favor of ZORA (zeroth-order regular approximation) for relativistic calculations [7] [54].
• Basis Set Adjustment: If insisting on Pauli formalism, increase frozen core sizes or reduce basis set flexibility, particularly for s- and p-functions [7].
• All-Electron Approach: Implement scalar relativistic all-electron approaches with appropriately constructed basis sets for spectroscopic parameter determination [54].

Optimization Instability with Near-180° Angles

Problem Description Geometry optimization becomes unstable when bond angles approach 180 degrees during the optimization process, particularly in large molecular fragments.

Diagnostic Steps

• Determine Initial Angle Values: Check if the initial angle was larger than 175° (receives special treatment) or became close to 180° during optimization (causes instability) [7].
• Identify Coordinate System: Determine if optimization uses Cartesian coordinates (requires more steps) versus delocalized coordinates [7].

Resolution Protocols

• Restart Optimization: Restart geometry optimization from the latest geometry to trigger special handling for near-180° angles [7].
• Constraint Application: As a last resort, constrain the angle to a value close to (but not equal to) 180 degrees [7].
• Coordinate System Change: Switch to delocalized internal coordinates for improved convergence behavior [7].

Frequently Asked Questions (FAQs)

What are the recommended basis sets for different molecular systems in SCF geometry optimization?

Table 1: Basis Set Selection Guide for Molecular Systems

Molecular System	Recommended Basis Sets	Key Considerations
Small organic molecules	3-21G, 6-31G, 6-311G	3-21G is most common for geometry optimization; 6-31G adds d-polarization for non-hydrogens and p-functions for hydrogens [55]
Transition metal complexes	cc-pVDZ, cc-pVTZ, TZ2P	Polarized triple-zeta sets recommended; include scalar relativistic effects for heavier elements [54]
Minimal basis applications	STO-3G	Use for qualitative results or very large molecules; provides lowest resolution/quality [55]
Correlation-intensive studies	aug-cc-pVDZ, aug-cc-pVTZ	Diffuse functions important for electron correlation effects; equivalent to 6-31+G(d) and 6-311+G(d) respectively [55]

How do I adjust SCF procedures for challenging convergence scenarios?

Accuracy Enhancement Protocol:

• Increase numerical quality to "good" [7]
• Add ExactDensity keyword or select "Exact" in "Density used in XC-potential" list (Note: increases computation time 2-3x) [7]
• Tighten SCF convergence criteria to 1e-8 [7]

Example Implementation:

What optimization algorithms show best performance for different molecular classes?

Table 2: Optimization Method Performance Across Molecular Classes

Method Class	Best Performing Systems	Limitations	Key References
Density Functional Theory (DFT)	Metal-radical systems (100-200 atoms), transition metal complexes	Pure functionals may overestimate covalency, bias toward low-spin states; hybrid functionals (B3LYP) preferred for spin-state energetics [54]	Neese et al. [54]
Hartree-Fock (HF)	Small to medium organic molecules, systems with minimal electron correlation	Default method in many packages; typically uses STO-3G if no basis set specified [55]	Pople et al. [55]
Quantum Algorithm Approaches	Small molecules (demonstrated with H₃⁺), minimal basis systems	Currently limited by qubit requirements; joint optimization of circuit and geometry parameters [56]	PennyLane Demos [56]
Molecular Mechanics	Very large systems, initial structure generation	Limited to molecular mechanics; exceptional structural parameters but no electronic properties [55]	Various [55]

How do I implement the quantum algorithm for molecular geometry optimization?

Workflow Overview:

Key Implementation Steps:

• Hamiltonian Construction: Build parametrized electronic Hamiltonian H(x) dependent on nuclear coordinates [56]
• Quantum Circuit Design: Prepare electronic trial state |Ψ(θ)⟩ using excitation operations (single and double excitations from Hartree-Fock reference) [56]
• Gradient Computation: Calculate nuclear gradients using ∇ₓg(θ,x) = ⟨Ψ(θ)|∇ₓH(x)|Ψ(θ)⟩ [56]
• Joint Optimization: Simultaneously optimize circuit parameters θ and nuclear coordinates x using gradient descent [56]

Example Code Framework:

What diagnostic tools are available for monitoring optimization progress?

Convergence Metrics:

• Energy Progression: Monitor energy changes over iterations - consistent directional change indicates progress toward minimum [7]
• Gradient Evolution: Track root-mean-square gradients - convergence indicated by values below threshold [57]
• Coordinate Changes: Monitor maximal atomic displacements between iterations [57]

Vibrational Analysis Validation:

• Perform frequency calculations upon optimization completion to confirm true minimum (no imaginary frequencies) [57]
• Obtain thermodynamic properties from vibrational analysis [57]

The Scientist's Toolkit: Research Reagent Solutions

Table 3: Essential Computational Tools for SCF Geometry Optimization

Tool/Resource	Function/Purpose	Application Context
TZ2P Basis Set	High-quality basis for accurate gradients; used with "Good" numerical quality	Systems requiring high accuracy in force calculations [7]
ExactDensity Keyword	Increases accuracy of density used in XC-potential	Challenging convergence cases; increases computation time 2-3x [7]
ZORA Relativistic Approximation	Handles relativistic effects for heavy elements	Systems containing 4d/5d transition metals, lanthanides, or actinides [7] [54]
OCCUPATIONS Block	Freezes electrons per symmetry	Prevents MO repopulation issues between geometries [7]
DoubleExcitation Gates	Quantum circuit components for electron correlation	Quantum algorithm implementations for molecular energy calculations [56]
STO-3G Minimal Basis	Rapid calculations for large systems or qualitative results	Initial structure screening, very large molecules [55]
6-31G Polarized Basis	Standard polarized basis for general organic molecules	Default-level calculations with polarization functions [55]

Experimental Protocol: Adaptive Quantum Circuit Selection

Purpose: Select optimal excitation operations for variational quantum circuits in molecular geometry optimization [56]

Methodology:

• Generate indices for all possible single- and double-excitations from Hartree-Fock reference state
• Construct initial circuit with all double-excitation gates
• Compute gradient of cost function with respect to each gate parameter
• Retain only gates with non-zero gradients
• Repeat process for single-excitation gates with selected double-excitation gates included
• Build final circuit with selected excitation operations

Implementation Example (H₃⁺ cation):

• Initial HF state: |110000⟩
• Selected double-excitations: [0, 1, 2, 3] and [0, 1, 4, 5]
• Final trial state: cos(θ₁)cos(θ₂)|110000⟩ - cos(θ₁)sin(θ₂)|000011⟩ - sin(θ₁)|001100⟩

Optimization Workflow Diagram

FAQs on Performance Metrics and Benchmarking

Q1: What are the key performance metrics for evaluating computational chemistry methods? Performance in computational chemistry is quantified using metrics that measure the accuracy, speed, and resource usage of calculations. Key metrics include [58]:

• Accuracy Metrics: For property prediction (e.g., energy differences), Mean Absolute Error (MAE) and Root Mean Squared Error (RMSE) are central. Lower values indicate higher accuracy. The Coefficient of Determination (R²) measures how well the method reproduces experimental trends, with values closer to 1.0 being better [59].
• Speed and Efficiency Metrics: Total execution time and the number of geometry optimization cycles to convergence are primary indicators of speed [58] [32].
• Reliability Metrics: The convergence success rate for Self-Consistent Field (SCF) and geometry optimization procedures is a critical measure of reliability [10] [32].
• Computational Cost: This is measured by resource utilization, including CPU hours, memory (RAM) consumption, and disk space usage [58] [60].

Q2: How do modern Neural Network Potentials (NNPs) compare to traditional DFT methods? Recent benchmarks on predicting experimental reduction potentials show that OMol25-trained NNPs can compete with or even surpass low-cost Density Functional Theory (DFT) methods for certain systems, though performance is highly model- and system-dependent [59].

The table below summarizes a benchmark study comparing methods on main-group (OROP) and organometallic (OMROP) reduction potential datasets [59]:

Table 1: Performance Benchmark of Computational Methods for Reduction Potential Prediction

Method	Dataset	MAE (V)	RMSE (V)	R²
B97-3c (DFT)	OROP	0.260	0.366	0.943
	OMROP	0.414	0.520	0.800
GFN2-xTB (SQM)	OROP	0.303	0.407	0.940
	OMROP	0.733	0.938	0.528
UMA-S (NNP)	OROP	0.261	0.596	0.878
	OMROP	0.262	0.375	0.896

Key findings from this study [59]:

• Trend for Organometallics: The UMA-S NNP was more accurate than GFN2-xTB and as accurate as B97-3c on organometallic species (OMROP), demonstrating the potential of NNPs for complex, charge-related properties in transition metal chemistry.
• Trend for Main-Group: For main-group molecules (OROP), the tested NNPs generally performed worse than traditional DFT and semi-empirical methods, indicating that system-specific benchmarking is crucial.

Q3: What are the target ranges for computational resource utilization? Efficient resource management is key for cost-effective research. The following table outlines general target utilization for computing resources, which helps in planning and optimizing calculations [61].

Table 2: Computational Resource Utilization Targets

Resource Type	Target Utilization	Optimization Benefit
CPU	60-80%	30-40% cost reduction via auto-scaling
Memory (RAM)	<75% capacity	25-35% cost reduction via right-sizing
Storage I/O	70-85%	20-30% cost reduction via tiered storage
Network	<60%	15-25% cost reduction via traffic optimization

Troubleshooting Guide: SCF and Geometry Optimization Convergence

Convergence issues are a common challenge in automated workflows. This guide provides a structured approach to diagnosing and resolving them.

Diagnostic Flowchart for Convergence Problems

The following diagram outlines a logical workflow for troubleshooting convergence issues in geometry optimization, synthesizing recommended practices from computational chemistry resources [10] [32] [6].

Frequently Asked Questions on Convergence

Q1: My SCF calculation will not converge. What are the first steps I should take? SCF convergence problems are common with open-shell systems and transition metal complexes [10]. Follow this systematic protocol:

• Verify System Definition: Ensure the molecular charge and spin multiplicity are correct. An incorrect number of unpaired electrons is a frequent cause of instability [32].
• Adjust SCF Algorithm Parameters:
  • Increase the maximum number of iterations (MaxIter 500) [10].
  • Use more conservative damping with keywords like SlowConv or VerySlowConv [10].
  • Increase the DIIS subspace size (e.g., DIISMaxEq 15) for difficult cases [10].
  • Apply a small level shift (e.g., Shift 0.1) to stabilize the SCF [10].
• Improve the Initial Guess: If the default guess (e.g., PModel) fails, try alternatives like HCore or PAtom [10]. For complex systems, a robust strategy is to:
  • Converge the SCF for a closed-shell cation or anion of the system.
  • Use the resulting orbitals as the starting guess (MORead) for the target open-shell system [10].
• Check for Numerical Issues: For density functional calculations, increasing the integration grid size can sometimes resolve convergence problems caused by numerical noise [10] [6].

Q2: My geometry optimization is oscillating or failing to converge. How can I fix it? A failing geometry optimization often stems from a poor initial structure or an inaccurate Hessian (second derivatives) [32].

• Re-examine the Starting Geometry: Ensure the initial molecular structure is chemically reasonable. Manually check bond lengths and angles. For difficult cases, disabling symmetry (IGNORESYMMETRY) or physically distorting the structure can help the optimizer find the true minimum [32].
• Improve the Initial Hessian: The most common fix is to use a better initial Hessian.
  • Use a conservative unit Hessian (HESS=UNIT) as a robust starting point [32].
  • For the best results, calculate a Hessian at a lower level of theory (e.g., semi-empirical or HF with a small basis set) and use it to start the optimization at the higher target level. This is done by running a frequency calculation first and then restarting the optimization [32].
• Adopt a Stepped Methodology: For challenging systems, especially large or complex molecules:
  • Start Simple: Optimize the geometry at a low level of theory (e.g., GFN2-xTB or HF/3-21G*).
  • Refine Stepwise: Use the optimized geometry from the lower level as the starting point for the higher-level calculation [32].
  • For large molecules, you can freeze the core parts of the molecule and optimize only the new or flexible regions before a final full optimization [32].

Q3: What specific strategies help with difficult systems like transition metals or large, flexible molecules? Systems with transition metals, open-shell states, or large conformational spaces require specialized strategies [10] [32]:

• For Transition Metal Complexes:
  • Use SlowConv and DIISMaxEq 15-40 [10].
  • Consider using the KDIIS algorithm, sometimes combined with SOSCF (but note that SOSCF can be unstable for open-shell systems and may require a delayed start with SOSCFStart 0.00033) [10].
  • Manually verify the expected spin state (high-spin vs. low-spin) and ensure the multiplicity is set correctly [32].
• For Large/Flexible Molecules:
  • The stepped methodology (Q2 above) is highly recommended.
  • Use internal coordinates for standard organic molecules but switch to Cartesian coordinates (NOGEOMSYMMETRY) for systems with high coordination numbers or when the bonding changes significantly during the optimization [32].
  • For transition state searches, a good initial guess for the Hessian is even more critical. The best practice is to compute a Hessian via a frequency calculation at a level close to the optimization theory [32].

The Scientist's Toolkit: Research Reagents & Computational Materials

This section details essential "research reagents" – the computational methods, models, and software components used in automated SCF convergence and benchmarking experiments.

Table 3: Essential Computational Tools for Automated SCF Research

Item Name	Function in Research	Example / Note
Neural Network Potentials (NNPs)	Fast, approximate energy/force calculators for screening and long molecular dynamics simulations.	OMol25-trained models (eSEN, UMA); accuracy is system-dependent [59].
Density Functional Theory (DFT)	The workhorse quantum mechanical method for geometry optimization and property calculation.	B97-3c, r2SCAN-3c, ωB97X-3c are popular for their balance of cost and accuracy [59].
Semiempirical Methods (SQM)	Very fast methods for initial geometry pre-optimization and conformational searching.	GFN2-xTB, g-xTB; requires self-interaction error correction for redox properties [59].
Benchmark Datasets	Standardized sets of molecules with reference data (e.g., energies, properties) for method validation.	OROP/OMROP (reduction potentials) [59]; Chen & Wentworth (electron affinities) [59].
Solvation Models	Account for solvent effects in calculated energies and properties.	CPCM-X, COSMO-RS; essential for predicting solution-phase properties like reduction potential [59].
SCF Convergers	Algorithms to solve the SCF equations. Choice depends on system difficulty.	DIIS, TRAH, KDIIS, MultiSecant; TRAH is robust but slower [10] [6].
Hessian/Preconditioner	Guides geometry optimization direction. Quality drastically affects convergence speed.	Default guess, Unit Hessian, Computed Hessian; a computed Hessian is most reliable [32].

Technical Support Center: SCF Convergence in Geometry Optimization

Frequently Asked Questions (FAQs)

FAQ 1: My geometry optimization of a drug-like molecule fails due to SCF non-convergence. What are the first steps I should try? Start with improving the initial electron-density guess. A poor initial guess is a common cause of failure. Use a converged wavefunction from a simpler method or basis set as a starting point via guess=read [4]. For systems with a small HOMO-LUMO gap, a frequent issue with transition metals in protein ligands, applying an energy level shift of 300-500 kcal/mol (SCF=vshift=400) can artificially increase the gap and prevent excessive orbital mixing, aiding convergence without affecting final results [4].

FAQ 2: How does the choice of SCF algorithm affect convergence for difficult protein-ligand complexes? The SCF algorithm is crucial for convergence efficiency and robustness. While DIIS (Direct Inversion in the Iterative Subspace) is fast and the default for many codes, it can be unstable for open-shell systems or those with small HOMO-LUMO gaps [11] [10]. For such difficult cases, second-order or geometric methods like Geometric Direct Minimization (GDM) or Trust Radius Augmented Hessian (TRAH) are more robust, though computationally more expensive [11] [10]. A recommended strategy is to start with DIIS and automatically switch to a more robust algorithm like GDM if convergence is slow [11].

FAQ 3: Why do my calculations on conjugated radical anions with diffuse functions consistently fail to converge? Systems like conjugated radical anions are pathologically difficult due to their diffuse electron density and near-degenerate orbitals. Standard DIIS procedures can fail. Specialized protocols are required, such as forcing a full rebuild of the Fock matrix in every SCF iteration (directresetfreq 1) to eliminate numerical noise and starting the Second-Order SCF (SOSCF) algorithm early with a reduced orbital gradient threshold [10].

FAQ 4: Are there specific strategies for converging SCF in open-shell transition metal complexes? Open-shell transition metal complexes are among the most challenging systems. They often require aggressive damping of the initial SCF iterations. Using built-in keywords like SlowConv or VerySlowConv applies strong damping [10]. Furthermore, increasing the number of previous Fock matrices used in the DIIS extrapolation (DIISMaxEq 15-40) enhances stability, and more frequent rebuilding of the Fock matrix can help [10].

Troubleshooting Guides

Guide 1: Resolving Oscillating or Slowly Converging SCF

Symptoms: The SCF energy oscillates wildly or the energy change (DeltaE) is decreasing very slowly without reaching the convergence threshold.

Procedure:

• Apply Damping: Use keywords like SlowConv to dampen large fluctuations in the initial SCF cycles [10].
• Adjust DIIS Parameters: Increase the size of the DIIS subspace (e.g., DIIS_SUBSPACE_SIZE 25) to use more historical data for a more stable extrapolation [11] [20].
• Reduce Fock Matrix Mixing: Lower the mixing parameter (e.g., to 0.015) to add a smaller fraction of the new Fock matrix to the guess for the next cycle, stabilizing the iteration [20].
• Enable Second-Order Methods: If the above fails, switch to a robust second-order converger like Geometric Direct Minimization (GDM) or Trust Radius Augmented Hessian (TRAH) [11] [10].

Guide 2: Recovering from SCF Convergence Failure in a Geometry Optimization

Symptoms: A geometry optimization job stops because the SCF failed to converge at one or more points along the path.

Procedure:

• Check Geometry Reasonableness: Verify that the geometry at the point of failure is physically realistic. Unreasonable bond lengths or angles can prevent convergence [20] [10].
• Reuse Orbitals: A moderately converged electronic structure from a previous geometry step is often a better initial guess. Ensure your optimization workflow is set to restart from the previous wavefunction [20].
• Simplify and Restart:
  • Converge the SCF for a simpler, related system (e.g., a cation instead of an anion, or using a lower-level theory like BP86/def2-SVP) [4].
  • Use the converged orbitals from this simpler calculation as the initial guess (guess=read or MORead) for the problematic geometry [4] [10].
• Modify SCF Settings: For the problematic step, implement more robust SCF settings, such as those outlined in Guide 1, and restart the optimization.

Experimental Protocols & Data

Protocol 1: Systematic SCF Convergence for High-Throughput Screening of Ligand Conformers

Aim: To generate a robust protocol for achieving SCF convergence across thousands of conformers of a drug-like molecule during an automated conformer search, as required for training and benchmarking neural network potentials (NNPs) [5].

Methodology:

• Initial Conformer Generation: Generate an initial ensemble of conformers using a stochastic method (e.g., via RDKit) or a metadynamics-based approach (e.g., CREST) [5].
• Two-Stage SCF Procedure:
  • Stage 1 (Fast Pre-optimization): For each conformer, attempt a rapid geometry optimization using a low-cost method (e.g., GFN2-xTB) or a fast NNP to relax the geometry.
  • Stage 2 (Robust DFT Single Point): For the pre-optimized geometries, perform a high-accuracy DFT single-point energy calculation using the following fallback strategy:
    • Primary Algorithm: DIIS with an increased subspace size.
    • Fallback Algorithm: If DIIS fails after 20 cycles, automatically switch to the GDM algorithm.
    • Initial Guess: Use the superposition of atomic densities (SAD) or a model potential guess for uniformity [5].
• Deduplication: Use a modular conformer-deduplication library to filter the final ensemble based on energy and structural similarity [5].

Protocol 2: SCF Convergence for Non-Covalent Interaction Energy Benchmarking

Aim: To ensure definitive SCF convergence when calculating interaction energies (E_int) for protein-ligand model systems (e.g., from the QUID benchmark set) at high levels of theory, where accuracy is critical [62].

Methodology:

• System Preparation: Use model dimer systems from a benchmark database like QUID, which represent diverse ligand-pocket interaction motifs (e.g., Ï€-stacking, H-bonding) [62].
• Initial Guess Strategy: For each dimer, perform a preliminary calculation at a lower but robust level of theory (e.g., PBE0+MBD). Use the resulting converged orbitals as the initial guess (guess=read) for the target high-accuracy calculation (e.g., ωB97M-V/def2-TZVPD or LNO-CCSD(T)) [48] [4] [62].
• Convergence Algorithm: Employ a second-order SCF algorithm (e.g., NEWTON_CG) from the outset to maximize the probability of convergence for these challenging, often weakly-bound, systems [11].
• Validation: Confirm that the final interaction energy is consistent with established benchmark values from the dataset to detect any potential convergence to an incorrect electronic state [62].

Table 1: Performance of SCF Convergence Accelerators on Different System Types

SCF Algorithm	Typical Use Case	Convergence Speed	Stability	Key Parameters to Adjust
DIIS [11] [10]	Standard organic molecules, closed-shell	Fast	Moderate	DIIS_SUBSPACE_SIZE (default 10-15), Cyc (startup cycles)
GDM [11]	Restricted open-shell, fallback option	Moderate	High	Built-in geometric parameters
TRAH [10]	Pathological cases (e.g., metal clusters)	Slow	Very High	AutoTRAHTOl (activation threshold), AutoTRAHIter
KDIIS+SOSCF [10]	Transition metal complexes	Fast (after SOSCF start)	High	SOSCFStart (orbital gradient threshold)
Level Shifting [4] [20]	Systems with small HOMO-LUMO gap	Varies	High	VShift (shift amount, typically 300-500)

Table 2: SCF Troubleshooting Settings for Common Problematic Systems

System Type	Primary Strategy	Specialized Settings / Keywords	Fallback Strategy
Transition Metal Complexes (Open-shell) [10]	Aggressive damping & larger DIIS space	SlowConv, DIISMaxEq 25, directresetfreq 5	KDIIS, SOSCFStart 0.00033
Systems with Diffuse Functions [4] [10]	Accurate integration & full Fock rebuild	int=ultrafine, SCF=NoVarAcc, directresetfreq 1	Level shifting (SCF=vshift=400)
Radical Anions [4] [10]	Converge cation first, read guess	Calculate cation, then guess=read	Fermi broadening (SCF=Fermi)
Pathological Cases (e.g., Fe-S clusters) [10]	Maximum stability settings	VerySlowConv, MaxIter 1500, DIISMaxEq 40, directresetfreq 1	Switch to TRAH or NEWTON_CG algorithm [11] [10]

Automated SCF Convergence Workflow

The following diagram illustrates a recommended automated workflow for handling SCF convergence within a geometry optimization run, incorporating the troubleshooting strategies detailed above.

The Scientist's Toolkit

Table 3: Essential Research Reagents & Computational Resources

Item Name	Type	Function / Application	Example / Reference
Open Molecules 2025 (OMol25) [48]	Dataset	Massive, diverse dataset of molecular DFT calculations for training and benchmarking ML potentials and SCF strategies on biomolecules, electrolytes, and metal complexes.	>100M calculations at ωB97M-V/def2-TZVPD [48]
QUID Benchmark [62]	Dataset	Provides robust benchmark interaction energies for ligand-pocket model systems, essential for validating methods on non-covalent interactions.	170 dimers with "platinum standard" LNO-CCSD(T) & FN-DMC energies [62]
Universal Model for Atoms (UMA) [48]	Neural Network Potential (NNP)	A pre-trained universal potential for fast and accurate energy/force evaluations, useful for generating initial guesses and pre-optimizing geometries.	Model trained on OMol25 and other datasets [48]
libxc [5]	Software Library	A portable, open-source library of exchange-correlation functionals, enabling modular and reproducible DFT code development.	Used by many quantum chemistry codes [5]
CREST [5]	Software	A metadynamics-based program for conformer searching and ranking, generating diverse structural ensembles for further study.	Integrated with the xTB semi-empirical package [5]
ωB97M-V/def2-TZVPD [48]	DFT Method/Basis Set	A high-accuracy, state-of-the-art density functional and basis set combination used for generating gold-standard reference data.	Used for the OMol25 dataset [48]

Technical support for comparing computational results with experimental data

Frequently Asked Questions (FAQs)

Q1: My optimized geometric parameters (bond lengths, angles) differ significantly from my experimental X-ray crystal structure. What could be the cause?

Several factors can contribute to discrepancies between computed gas-phase geometries and solid-state X-ray data. First, computational methods typically calculate energies for isolated molecules, while X-ray structures are influenced by crystal packing forces that can distort molecular geometry. Second, ensure your computational method accounts for the correct electronic state; for example, open-shell systems require unrestricted DFT formalisms. Finally, the choice of basis set and density functional can significantly impact results. Using a larger basis set (e.g., triple-zeta) and a functional known for accurate structural prediction is recommended.

Q2: My calculated NMR chemical shifts do not match the experimental spectrum. How can I improve the agreement?

Start by verifying that the computed geometry is a true minimum on the potential energy surface by confirming the absence of imaginary frequencies in the vibrational analysis. NMR properties are sensitive to the molecular geometry. Secondly, ensure you are using a method and basis set appropriate for NMR prediction, often involving a hybrid or double-hybrid functional and a basis set with polarization functions. Finally, remember that calculated shifts are typically referenced to a standard compound (e.g., TMS for 1H and 13C); the chosen reference and its calculated value must align with your experimental setup.

Q3: My simulated UV-Vis spectrum shows a shifted absorption maximum compared to the experimental solution spectrum. Why?

The primary reason is often the solvation effect. Computational simulations often occur in the gas phase, while experimental measurements are conducted in solution. Incorporate a solvation model (e.g., PCM, SMD) into your calculation to account for solvent-solute interactions. Additionally, the choice of functional is critical for excited states. Functionals like CAM-B3LYP or wB97XD are often better suited for charge-transfer excitations. The number of excited states calculated and the inclusion of vibrational broadening in your simulation also affect the spectral shape and peak position.

Q4: My SCF calculation fails to converge during the geometry optimization of a transition metal complex. What are my options?

Transition metal complexes with localized open-shell configurations are notoriously difficult to converge [20]. A multi-pronged approach is effective:

• Improve the Initial Guess: Use the electron density from a previously converged calculation of a similar structure or a fragment of your molecule as a restart [20].
• Change the SCF Algorithm: Switch from the default DIIS algorithm to a more robust one like Geometric Direct Minimization (GDM) [11] or the Augmented Roothaan-Hall (ARH) method [20].
• Use Smearing: Apply a small amount of electron smearing to occupy near-degenerate levels, which is particularly helpful for systems with a small HOMO-LUMO gap [20].
• Simplify and Restart: Converge the system with a smaller basis set first, then use the resulting orbitals as a guess for a calculation with the larger, target basis set [63].

Q5: How do I know if my calculated vibrational frequencies are reliable?

A key initial check is to confirm that your optimized geometry is a true minimum, indicated by the absence of imaginary frequencies. The scale factor for your chosen functional/basis set combination must be applied for quantitative agreement with experiment, as harmonic frequencies calculated by DFT are typically overestimated. For comparison with experimental IR spectra, ensure that the calculated intensities match the observed band strengths, not just the peak positions.

Troubleshooting Guide: Computational-Experimental Mismatches

Problem Area	Potential Computational Cause	Experimental Consideration	Corrective Action
Geometry	- Wrong functional/basis set- Gas-phase vs. crystal environment	- Crystal packing forces- Thermal motion	- Use a dispersion-corrected functional- Perform a periodic calculation for solids
NMR Shifts	- Incorrect reference compound- Insufficient geometry optimization	- Concentration effects- pH sensitivity	- Re-calculate reference with same method- Ensure geometry is a minimum energy structure
UV-Vis Spectrum	- Lack of solvation model- Inappropriate functional for excitations	- Solvent polarity- Sample impurities	- Include an explicit solvation model- Use a range-separated functional
IR Spectrum	- Lack of anharmonicity- Ignoring scale factors	- Phase difference (gas vs. solid)- Water vapor interference	- Apply a standard scale factor- Compare relative peak positions, not absolute

Research Reagent Solutions: Computational and Experimental Tools

Item	Function in Validation
Polarizable Continuum Model (PCM)	Implicit solvation model to simulate the effect of a solvent on computed spectroscopic properties.
Dispersion-Corrected Density Functional (e.g., ωB97X-D)	A density functional that includes corrections for van der Waals forces, crucial for accurate geometric parameters, especially in stacked or layered systems.
NMR Reference Compound (e.g., TMS)	A standard compound used to calibrate the chemical shift scale in both experimental and computational NMR spectroscopy.
Deuterated Solvent (e.g., CDCl₃)	Solvent used in experimental NMR spectroscopy; its properties can be modeled computationally for direct comparison.
CIF (Crystallographic Information File)	The standard file format for X-ray crystallographic data, containing the experimental atomic coordinates used for comparison.
SCF Convergence Accelerator (e.g., GDM, DIIS)	Algorithms that help achieve a self-consistent solution for the electron density, which is a prerequisite for any property calculation [11].

Workflow for Computational-Experimental Validation

The following diagram outlines a systematic workflow for validating computational results against experimental data, integrating key decision points and troubleshooting steps.

Advanced SCF Convergence for Challenging Systems

For complex systems like open-shell transition metal complexes, standard convergence protocols often fail. The diagram below guides the selection of advanced algorithms and techniques to achieve convergence.

SCF Convergence Algorithm Comparison

Algorithm	Typical Use Case	Key Parameters to Adjust	Pros & Cons
DIIS [11]	Default for most systems; fast convergence when near solution.	DIIS_SUBSPACE_SIZE, Mixing [20]	Pro: Very efficient. Con: Can oscillate or diverge for difficult cases.
GDM [11]	Fallback when DIIS fails; restricted open-shell calculations.	Convergence tolerances (TolE, TolG) [22]	Pro: Highly robust. Con: Slightly less efficient than DIIS.
ARH [20]	Difficult systems where other accelerators fail.	Trust radius, convergence criteria.	Pro: Direct energy minimization, very stable. Con: Computationally more expensive.
Electron Smearing [20]	Metallic systems or those with very small HOMO-LUMO gaps.	Smearing width (electronic temperature).	Pro: Helps overcome convergence barriers. Con: Alters total energy; keep parameter low.

Convergence Level	Energy Change (TolE)	Max Density Change (TolMaxP)	DIIS Error (TolErr)	Recommended Use
Loose	1e-5	1e-3	5e-4	Initial geometry scans, large systems.
Medium (Default)	1e-6	1e-5	1e-5	Standard single-point energy calculations.
Tight	1e-8	1e-7	5e-7	Geometry optimizations, transition metal complexes.
VeryTight	1e-9	1e-8	1e-8	Frequency calculations, final energy values.

Frequently Asked Questions (FAQs)

Q1: What are the first steps I should take if my geometry optimization does not converge?

A1: First, analyze the behavior of the energy during the latest iterations. If the energy is changing consistently in one direction, your starting geometry was likely far from a minimum; simply increasing the allowed number of iterations and restarting from the latest geometry may suffice. If the energy oscillates around a value, the problem may lie with the accuracy of the calculated forces. Initial remedies include increasing the numerical quality, tightening the SCF convergence criteria, or using an exact density calculation to improve gradient accuracy [7].

Q2: My SCF calculation oscillates wildly and will not converge. What strategies can I employ?

A2: For oscillating SCF procedures, consider switching to a more stable, conservative convergence algorithm. You can reduce the DIIS mixing parameter (e.g., to 0.015) and increase the number of DIIS expansion vectors (e.g., to 25) to make the process more stable [20]. Alternatively, try different built-in algorithms like MESA, LISTi, or the second-order TRAH method, which are designed for difficult cases [20] [10]. Electron smearing or level shifting can also help overcome convergence issues, particularly in systems with a small HOMO-LUMO gap [20].

Q3: How can I validate that my virtual cohort or in-silico trial is producing reliable results?

A3: You can use open-source statistical environments, such as the R-Shiny application developed in the SIMCor project. This tool provides a menu-driven platform to compare virtual cohorts with real-world datasets using established statistical techniques. It supports the entire validation workflow, helping to ensure your in-silico models are robust and credible before use in critical applications like drug and medical device development [64].

Q4: I am using a large basis set and the calculation fails due to "linear dependencies." What does this mean and how can I fix it?

A4: This error indicates that your basis set is too diffuse for the system, creating numerically redundant functions. This is common with heavy elements or large, diffuse basis sets like aug-cc-pVTZ. Instead of loosening the dependency criterion, which is not recommended, you should adjust the basis set itself. Applying spatial confinement to reduce the range of the most diffuse basis functions or manually removing certain functions are effective strategies to resolve this [6].

Troubleshooting Guides

Troubleshooting SCF Convergence Failure

Self-Consistent Field (SCF) convergence is a common challenge, especially for systems with transition metals, open-shell configurations, or small HOMO-LUMO gaps [20] [10]. Follow this systematic guide to resolve SCF issues.

Table: SCF Convergence Algorithms and Their Applications

Algorithm/Method	Description	Best For	Key Input Example (ORCA)
DIIS	Standard, fast extrapolation method.	Standard closed-shell molecules [10].	Default
KDIIS+SOSCF	Combines KDIIS with the Second-Order SCF method.	Faster convergence for some systems [10].	! KDIIS SOSCF
TRAH	Robust, second-order converger (Trust Radius Augmented Hessian).	Pathological cases; automatically activates in ORCA if DIIS struggles [10].	! NoTrah (to disable)
MultiSecant	Alternative to DIIS at no extra cost per cycle.	Systems where DIIS fails [6].	SCF\n Method MultiSecant\nEnd (BAND)

Protocol: A Step-by-Step Guide to Converging a Difficult SCF

• Verify the Basics: Ensure your molecular geometry is reasonable and uses the correct units. Confirm the spin multiplicity (e.g., restricted vs. unrestricted) is physically correct for your system [20].
• Improve the Initial Guess: A better starting point can be achieved by:
  • Using the PAtom or Hueckel guess instead of the default [10].
  • Running a preliminary calculation with a smaller basis set (e.g., def2-SVP) and reading its orbitals for a more complex calculation (! MORead in ORCA) [10] [6].
  • Converging a closed-shell cation/anion of your system and using its orbitals as the guess [10].
• Adjust SCF Algorithm Parameters: For oscillating cases, apply more conservative settings.
  • ORCA: Use the ! SlowConv or ! VerySlowConv keywords, which automatically apply damping. For extreme cases, manually increase DIISMaxEq (e.g., to 15) and set directresetfreq to 1 to eliminate numerical noise [10].
  • ADF/BAND: Reduce the SCF%Mixing value and disable adaptable DIIS (Diis\n Adaptable false\nEnd) [6].
• Employ Advanced Techniques: If the above fails, consider these options, keeping in mind they may alter results and require validation:
  • Electron Smearing: Apply a small finite electronic temperature (e.g., Convergence ElectronicTemperature 0.01) to populate orbitals around the Fermi level, which can break degeneracy issues [20] [6].
  • Level Shifting: Artificially raise the energy of virtual orbitals to prevent occupation cycling [20].

The workflow for this troubleshooting process is summarized in the following diagram:

Troubleshooting Geometry Optimization Failure

When a geometry optimization fails to converge, the problem often originates from the underlying SCF or from inaccurate gradients.

Protocol: Systematic Geometry Optimization Troubleshooting

• Ensure SCF Convergence: A geometry optimization cannot converge if the SCF energy at each point is not reliable. Follow the SCF troubleshooting guide above to ensure the SCF is fully converged at every step of the optimization [7] [10].
• Improve Gradient Accuracy: Inaccurate forces lead the optimizer astray. To improve gradient accuracy:
  • Increase the numerical integration quality (e.g., NumericalQuality Good).
  • Tighten the SCF convergence criterion (e.g., SCF\n converge 1e-8\nEnd).
  • Use an exact density calculation (ExactDensity), though this is computationally expensive [7].
• Check for Problematic Geometries: Optimization can become unstable when angles approach 180 degrees during the process (as opposed to starting near 180). If this occurs, restart the optimization from the latest geometry. As a last resort, constrain the angle to a value close to, but not exactly, 180 degrees [7].
• Change Optimization Coordinates: For molecular systems, using delocalized internal coordinates (as in ADF) often leads to faster and more stable convergence compared to Cartesian coordinates [7].
• Use Automation for Difficult Cases: For complex optimizations (e.g., a molecule on a slab), you can automate the relaxation of convergence criteria at the start. Configure the optimizer to use a looser SCF criterion and higher electronic temperature when gradients are large, automatically tightening them as the geometry refines [6].

Table: Common Geometry Optimization Issues and Solutions

Problem	Possible Cause	Recommended Solution
Bonds are too short	Basis set superposition error (BSSE); frozen core approximation failure; use of Pauli relativistic method [7].	Switch to ZORA relativistic approach; use bigger frozen cores or a reduced basis set [7].
Optimization oscillates	Inaccurate gradients; SCF not fully converged; problematic constraints [7].	Improve gradient accuracy (Step 2 above); ensure SCF convergence; check that constraints do not break symmetry [7].
Negative frequencies	Geometry not a true minimum; phonon calculation step size too large [6].	Re-optimize geometry to a minimum; reduce step size in phonon calculation [6].

The Scientist's Toolkit: Research Reagent Solutions

Table: Essential Open-Source Tools and Computational Resources

Tool/Resource	Function	Application in Validation
R-Shiny (SIMCor)	An open-source statistical web application for the validation of virtual cohorts [64].	Provides a menu-driven environment to statistically compare virtual cohort outputs with real-world clinical data, ensuring the cohort's representativeness [64].
Valsci	An open-source utility for automated large-batch scientific claim verification using LLMs [65].	Automates the process of verifying scientific claims or hypotheses against the published literature, reducing manual review time and minimizing citation hallucinations [65].
SCM (ADF/BAND)	A commercial modeling suite with extensive, publicly available documentation on troubleshooting DFT calculations [7] [20] [6].	Its documentation serves as a key community resource for understanding and resolving common pitfalls in SCF and geometry optimization.
ORCA Input Library	A community-driven website compiling tips and input examples for the ORCA software [10].	Provides practical, peer-shared configurations for converging difficult systems like open-shell transition metal complexes.
Great Expectations	An open-source Python library for validating, documenting, and profiling data [66] [67].	Can be integrated into computational workflows to automatically validate that input and output data (e.g., molecular geometries, energies) meet predefined "expectations," ensuring pipeline data quality [67].

Conclusion

Automating SCF convergence is paramount for achieving robust, high-throughput geometry optimizations in computational drug discovery and biomolecular research. By integrating foundational understanding with advanced algorithms, systematic troubleshooting protocols, and rigorous validation frameworks, researchers can significantly enhance computational reliability. Future advancements in machine learning–initialized guesses, adaptive algorithm selection, and specialized implicit solvent models promise to further automate these workflows. These developments will enable more accurate prediction of molecular structures and interactions, accelerating rational drug design and the understanding of complex biological systems at the atomic level.

References

• 1. Introducing Open Molecules 2025: A massive dataset for ... [https://www.linkedin.com/posts/samuel-blau_the-open-molecules-2025-dataset-is-out-with-activity-7328461647461654529-ToOx]
• 2. What are the physical reasons if the SCF doesn't converge? [https://mattermodeling.stackexchange.com/questions/8635/what-are-the-physical-reasons-if-the-scf-doesnt-converge]
• 3. Issue with S₁ State Optimization Under PCM – SCF ... [https://talk.q-chem.com/t/issue-with-s-state-optimization-under-pcm-scf-convergence-error/2958]
• 4. Methods to Solve the SCF not Converged | Zhe WANG, Ph.D. [https://wongzit.github.io/method-to-solve-the-scf-not-converged/]
• 5. Open-Source Projects We Wish Existed - Rowan Scientific [https://rowansci.com/blog/open-source-projects-we-wish-existed]
• 6. Troubleshooting — BAND 2025.1 documentation - SCM [https://www.scm.com/doc/BAND/Troubleshooting/Trouble_Shooting.html]
• 7. Geometry Optimization troubleshooting — ADF 2025.1 ... - SCM [https://www.scm.com/doc/ADF/Rec_problems_questions/Geometry_Optimization.html]
• 8. Troubleshooting electronic convergence - VASP Wiki [https://vasp.at/wiki/Troubleshooting_electronic_convergence]
• 9. Why do I see Oscillations in energy using SCF Hartree ... [https://physics.stackexchange.com/questions/354404/why-do-i-see-oscillations-in-energy-using-scf-hartree-fock-approximation]
• 10. SCF Convergence Issues - ORCA Input Library [https://sites.google.com/site/orcainputlibrary/scf-convergence-issues]
• 11. 4.5 Converging SCF Calculations [https://manual.q-chem.com/5.1/sect-convergence.html]
• 12. Molecular modeling and simulation of some efficient ... [https://www.sciencedirect.com/science/article/abs/pii/S235249281930755X]
• 13. Starting SCF Calculations by Superposition of Atomic ... [https://pubmed.ncbi.nlm.nih.gov/16557519/]
• 14. Unifying machine learning and quantum chemistry with a ... [https://www.nature.com/articles/s41467-019-12875-2]
• 15. OpenOrbitalOptimizer—a reusable open source library for ... [https://arxiv.org/html/2503.23034v1]
• 16. Geometry optimization — AMS 2025.1 documentation - SCM [https://www.scm.com/doc/AMS/Tasks/Geometry_Optimization.html]
• 17. Efficient implementation of the superposition of atomic ... [https://arxiv.org/abs/2002.02587]
• 18. 4.5.3 Direct Inversion in the Iterative Subspace (DIIS) [https://manual.q-chem.com/5.4/sect_diis.html]
• 19. Application of the DIIS technique to improve ... [https://www.sciencedirect.com/science/article/abs/pii/S0166128001005024]
• 20. SCF Convergence Guidelines for ADF - SCM [https://www.scm.com/doc/ADF/Rec_problems_questions/SCF.html]
• 21. The DePrince Research Group [https://www.chem.fsu.edu/~deprince/programming_projects/diis/]
• 22. 7.7. SCF Convergence - ORCA 6.0 Manual [https://www.faccts.de/docs/orca/6.0/manual/contents/detailed/scfconv.html]
• 23. 6.3. Geometry Optimizations, Surface Scans, Transition ... [https://www.faccts.de/docs/orca/6.0/manual/contents/typical/optimizations.html]
• 24. Issues with SCF convergence with organometallic ... [https://github.com/grimme-lab/xtb/issues/952]
• 25. Self-consistent field (SCF) methods [https://pyscf.org/user/scf.html]
• 26. Approximate second-order SCF convergence for spin ... [https://www.sciencedirect.com/science/article/abs/pii/S000926140000662X]
• 27. Comparison of self-consistent field convergence ... [https://pubmed.ncbi.nlm.nih.gov/22894335/]
• 28. SCF [https://gaussian.com/scf/]
• 29. 4.5.7 Geometric Direct Minimization (GDM) [https://manual.q-chem.com/5.3/sect_gdm.html]
• 30. 4.5 Converging SCF Calculations [https://manual.q-chem.com/4.3/sect-convergence.html]
• 31. 4.5.4 Geometric Direct Minimization (GDM) [https://manual.q-chem.com/5.2/Ch4.S5.SS4.html]
• 32. Convergence Questions [https://downloads.wavefun.com/FAQ/converge.html]
• 33. Different (larger) SCF energy compared to other software ... [https://talk.q-chem.com/t/different-larger-scf-energy-compared-to-other-software-orca-c4-when-using-an-augmented-aug-cc-pvdz-basis-set/2905]
• 34. SCF — ADF 2025.1 documentation - SCM [https://www.scm.com/doc/ADF/Input/SCF.html]
• 35. Scf convergence issue - Questions [https://talk.q-chem.com/t/scf-convergence-issue/1503]
• 36. Car-Parrinello Monitor for more robust Born-Oppenheimer ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC9749491/]
• 37. Geometry Optimization Algorithms in Conjunction with the ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC11201553/]
• 38. Accelerating self-consistent field convergence with the ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC2830258/]
• 39. Dealing with Complexity in Open-Shell Transition Metal ... [https://www.sciencedirect.com/science/article/abs/pii/S0898883810620089]
• 40. The trouble with transition metals II: SCF convergence [http://molecularmodelingbasics.blogspot.com/2009/11/trouble-with-transition-metals-ii-scf.html]
• 41. A Comparison of Different Open-Source Geometry Optimizers [https://pubmed.ncbi.nlm.nih.gov/37870541/]
• 42. Which Optimizer Should You Use With NNPs? | Rowan [https://www.rowansci.com/blog/which-optimizer-should-you-use-with-nnps]
• 43. 2.6. Self-Consistent-Field (SCF) [https://orca-manual.mpi-muelheim.mpg.de/contents/essentialelements/scf.html]
• 44. HF: Hartree–Fock Theory [https://psicode.org/psi4manual/1.9.x/scf.html]
• 45. Convergence Tips [https://suncat.stanford.edu/wiki/convergence-tips]
• 46. Self Consistent Field (SCF) — BAND 2025.1 documentation [https://www.scm.com/doc/BAND/Accuracy_and_Efficiency/SCF.html]
• 47. basis set superposition error (BSSE) [https://www.cup.uni-muenchen.de/ch/compchem/basis/bsse1.html]
• 48. Exploring Meta's Open Molecules 2025 (OMol25) & Universal ... [https://www.rowansci.com/blog/exploring-open-molecules-2025]
• 49. A Record-Breaking Dataset to Train AI Models has Launched [https://newscenter.lbl.gov/2025/05/14/computational-chemistry-unlocked-a-record-breaking-dataset-to-train-ai-models-has-launched/]
• 50. Automatic Optimization of PAW Pseudopotentials [https://tech.preferred.jp/en/blog/automatic-optimization-of-paw-pseudopotentials/]
• 51. Modeling extensive defects in metals through classical ... [https://www.nature.com/articles/s41524-025-01599-1]
• 52. Adaptive Parameters Methods for Machine Learning [https://towardsdatascience.com/adaptive-parameters-methods-for-machine-learning-6f7101a9a71/]
• 53. Designing an adaptive learning framework for predicting ... [https://www.sciencedirect.com/science/article/abs/pii/S0952197624016300]
• 54. Geometry Optimization - an overview [https://www.sciencedirect.com/topics/engineering/geometry-optimization]
• 55. Comparison of Molecular Geometry Optimization Methods ... [https://www.mdpi.com/2227-7390/9/22/2855]
• 56. Optimization of molecular geometries | PennyLane Demos [https://pennylane.ai/qml/demos/tutorial_mol_geo_opt/]
• 57. Geometry Optimization: Precision in Molecular Structure ... [https://www.promethium.qcware.com/geometry-optimization]
• 58. Performance Metric - an overview | ScienceDirect Topics [https://www.sciencedirect.com/topics/computer-science/performance-metric]
• 59. Benchmarking OMol25-Trained Models on Experimental ... [https://rowansci.com/publications/omol25-redox]
• 60. Computer performance [https://en.wikipedia.org/wiki/Computer_performance]
• 61. A Guide to Essential Metrics for Success [https://7t.ai/blog/ai-performance-metrics-7tt/]
• 62. Extending quantum-mechanical benchmark accuracy to ... [https://www.nature.com/articles/s41467-025-63587-9]
• 63. Convergence Tricks – Kate Penrod CoMET Capstone [https://sites.psu.edu/penrodcapstone/convergence/]
• 64. An open source statistical web application for validation ... [https://www.nature.com/articles/s41598-025-99720-3]
• 65. Valsci: an open-source, self-hostable literature review utility ... [https://bmcbioinformatics.biomedcentral.com/articles/10.1186/s12859-025-06159-4]
• 66. 7 Open-Source Data Quality Tools to Use in 2025 [https://dqops.com/open-source-data-quality-tools/]
• 67. 5 Open Source Data Quality Tools – 2024 Edition [https://datacoves.com/post/data-quality-tools]